题目内容
1.调查者通过询问64名男女大学生在购买食品时是否看营养说明,得到的数据如表所示:| 看营养说明 | 不看营养说明 | 合计 | |
| 男大学生 | 26 | 6 | 32 |
| 女大学生 | 14 | 18 | 32 |
| 合计 | 40 | 24 | 64 |
附:参考公式与数据:χ2=$\frac{{n{{(n}_{11}n}_{22}{{-n}_{12}n}_{21})}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$.当χ2>3.841时,有95%的把握说事件A与B有关;当χ2>6.635时,有99%的把握说事件A与B有关;当χ2≤3.841时,有95%的把握说事件A与B是无关的.
分析 根据表中数据,计算观测值,对照临界值即可得出结论.
解答 解:根据表中数据,计算
χ2=$\frac{{n{{(n}_{11}n}_{22}{{-n}_{12}n}_{21})}^{2}}{{n}_{1}{+n}_{2}{{+n}_{+1}n}_{+2}}$=$\frac{64{×(26×18-14×6)}^{2}}{40×24×32×32}$=9.6>6.635,
有99%的把握说大学生的性别与是否看营养说明之间有关系.
点评 本题考查了独立性检验的应用问题,是基础题.

练习册系列答案
相关题目
16.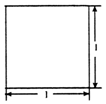 若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
 若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )
若一个底面是等腰直角三角形的直三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为( )| A. | 6π或5π | B. | 3π或5π | C. | 6π | D. | 5π |
6.已知函数f(x)=asinx+bcosx(x∈R),若x=x0是函数f(x)的一条对称轴,且tanx0=3,则点(a,b)所在的直线为( )
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
13.已知某条曲线的参数方程是$\left\{\begin{array}{l}x=2(t+\frac{1}{t})\\ y=2(t-\frac{1}{t})\end{array}$(t是参数),则该曲线是( )
| A. | 直线 | B. | 圆 | C. | 椭圆 | D. | 双曲线 |
11.把函数f(x)=cos2($\frac{π}{2}$x-$\frac{π}{6}$)的图象向左平移$\frac{1}{3}$个单位后得到的函数为g(x),则以下结论中正确的是( )
| A. | g($\frac{1}{5}$)>g($\frac{8}{5}$)>0 | B. | g($\frac{1}{5}$)$>0>g(\frac{8}{5})$ | C. | g($\frac{8}{5}$)>g($\frac{1}{5}$)>0 | D. | g($\frac{1}{5}$)=g($\frac{8}{5}$)>0 |
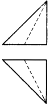
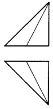
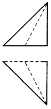
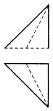
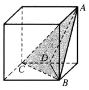 如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )
如图是一个正方体,A,B,C为三个顶点,D是棱的中点,则三棱锥A-BCD的正视图,俯视图是(注:选项中的上图是正视图,下图是俯视图)( )