题目内容
17.函数f(x)=x2e-x,则函数f(x)的极小值是0.分析 通过求导判断函数的单调性,结合极小值的概念可得结论.
解答 解:因为f(x)=x2e-x,x∈R
所以f′(x)=2xe-x-x2e-x=(2-x)xe-x,
令f′(x)=0,解得x=0或x=2,
因为当x<0或x>2时f′(x)<0,当0<x<2时f′(x)>0,
所以函数f(x)的单调递增区间为(0,2),单调递减区间为(-∞,0),(2,+∞),
所以当x=0时取得极小值f(0)=0,
故答案为:0.
点评 本题考查利用导数研究函数的极值,考查运算求解能力,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
6.已知函数f(x)=asinx+bcosx(x∈R),若x=x0是函数f(x)的一条对称轴,且tanx0=3,则点(a,b)所在的直线为( )
| A. | x-3y=0 | B. | x+3y=0 | C. | 3x-y=0 | D. | 3x+y=0 |
7.设P是曲线y=x-$\frac{1}{2}$x2-lnx上的一个动点,记此曲线在点P点处的切线的倾斜角为θ,则θ的取值范围是( )
| A. | ($\frac{π}{2}$,$\frac{3π}{4}$] | B. | [$\frac{π}{4}$,$\frac{3π}{4}$] | C. | [$\frac{3π}{4}$,π) | D. | [0,$\frac{π}{2}$)∪[$\frac{3π}{4}$,π) |
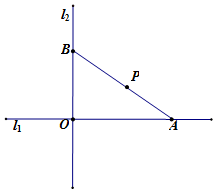 如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点.
如图所示,互相垂直的两条道路l1、l2相交于O点,点P与l1、l2的距离分别为2千米、3千米,过点P建一条直线道路AB,与l1、l2分别交于A、B两点. 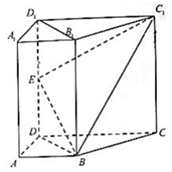 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.