题目内容
 某建筑的金属支架如图所示,根据要求AB至少长2.8米,C为AB的中点,B到D的距离比CD的长小0.5m,∠BCD=60°,已知建筑支架的材料每米的价格为每米100元.
某建筑的金属支架如图所示,根据要求AB至少长2.8米,C为AB的中点,B到D的距离比CD的长小0.5m,∠BCD=60°,已知建筑支架的材料每米的价格为每米100元.(1)设BC=x米,CD=y米,试用x表示y;
(2)问怎样设计AB,CD的长,可使建造这个支架的成本最低,并求最低成本是多少元?
考点:基本不等式在最值问题中的应用
专题:综合题,不等式的解法及应用
分析:(1)△BCD中,BC=x,CD=y,∠BCD=60°,由余弦定理可得x,y的关系式;
(2)由造价函数:W=100(2x+y)=100(2x+
),不妨设t=x-1,那么t≥0.4,化简W为t的函数容易求出结果.
(2)由造价函数:W=100(2x+y)=100(2x+
| x2-0.25 |
| x-1 |
解答:
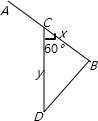 解:(1)如图,由余弦定理得:(y-0.5)2=x2+y2-2xycos60°,
解:(1)如图,由余弦定理得:(y-0.5)2=x2+y2-2xycos60°,
∴y=
(其中x≥1.4);
(2)设支架的造价为:W=100(2x+y)=100(2x+
),
设t=x-1,那么t≥0.4,∴W=100(3t+
+4)≥700,
当且仅当t=0.5>0.4,x=1.5,y=4时,这时造价W的值也最小,且有AB=3米,CD=4米.
 解:(1)如图,由余弦定理得:(y-0.5)2=x2+y2-2xycos60°,
解:(1)如图,由余弦定理得:(y-0.5)2=x2+y2-2xycos60°,∴y=
| x2-0.25 |
| x-1 |
(2)设支架的造价为:W=100(2x+y)=100(2x+
| x2-0.25 |
| x-1 |
设t=x-1,那么t≥0.4,∴W=100(3t+
| 3 |
| 4t |
当且仅当t=0.5>0.4,x=1.5,y=4时,这时造价W的值也最小,且有AB=3米,CD=4米.
点评:本题借助三角形的余弦定理建立函数解析式,考查函数的最值问题,是中档题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
到两坐标轴距离相等的点的轨迹方程是( )
| A、y=x |
| B、x2-y2=0 |
| C、y=-x |
| D、y=|x| |
 如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.
如图,设AD是△ABC的角平分线,AD交△ABC的外接圆与点E.求证:AB•AC=AD•AE.