Question

已知函数f（x）=

3-x2，x∈[-1，2] x-3，x∈(2，5]

．
（1）在图中给定的直角坐标系内画出f（x）的图象；
（2）写出f（x）的单调区间；
（3）解不等式f（x）＜2．

Answer 1

考点：二次函数的性质

专题：函数的性质及应用

分析：（1）在所给的坐标系中作出函数f（x）=

3-x2，x∈[-1，2] x-3，x∈(2，5]

的图象．
（2）结合函数f（x）的图象可得函数f（x）的增区间和减区间．
（3）由不等式f（x）＜2，结合函数f（x）的图象可x的范围．

解答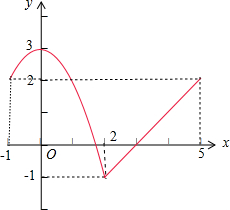： 解：（1）在所给的坐标系中作出函数f（x）=

3-x2，x∈[-1，2] x-3，x∈(2，5]

的图象，如图：
（2）结合函数f（x）的图象可得函数f（x）的增区间为：[-1 0）、[2，5]；
减区间为：（0，2）．
（3）由不等式f（x）＜2，结合函数f（x）的图象可得1＜x＜5，
故要求的不等式的解集为（1，5）．

点评：本题主要考查作函数的图象，分段函数的应用，函数的图象特征，二次函数的性质，属于基础题．