题目内容
已知双曲线C的中心是原点,右焦点为F(
,0).
(1)当双曲线C的离心率e=
(2),求此双曲线C的标准方程;
(3)若双曲线C的一条渐近线方程为X+
Y=0,求此双曲线C的标准方程.
| 3 |
(1)当双曲线C的离心率e=
| 3 |
(3)若双曲线C的一条渐近线方程为X+
| 2 |
考点:双曲线的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)依题意设双曲线C的方程为
-
=1(a>0,b>0),由已知得c=
,e=
=
,由此能求出双曲线C的标准方程.
(2)设双曲线C的方程为x2-2y2=λ(λ>0),由已知得λ+
=3,由此能求出双曲线C的方程.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| c |
| a |
| 3 |
(2)设双曲线C的方程为x2-2y2=λ(λ>0),由已知得λ+
| λ |
| 2 |
解答:
解:(1)依题意设双曲线C的方程为
-
=1(a>0,b>0)…(1分)
∵c=
,e=
=
,∴a=1,b=
…(4分)
∴双曲线C的标准方程为x2-
=1…(6分)
(2)设双曲线C的方程为x2-2y2=λ(λ>0),…(8分)
∴λ+
=3,解得λ=2,…(11分)
∴双曲线C的标准方程为
-y2=1.…(13分)
| x2 |
| a2 |
| y2 |
| b2 |
∵c=
| 3 |
| c |
| a |
| 3 |
| 2 |
∴双曲线C的标准方程为x2-
| y2 |
| 2 |
(2)设双曲线C的方程为x2-2y2=λ(λ>0),…(8分)
∴λ+
| λ |
| 2 |
∴双曲线C的标准方程为
| x2 |
| 2 |
点评:本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,注意双曲线性质的合理运用.

练习册系列答案
相关题目
在△ABC中,AC=2,BC=1,cosC=
,则△ABC的面积为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
 已知函数f(x)=
已知函数f(x)=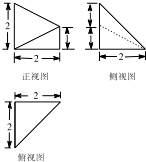 某几何体的三视图如图所示,该几何体的表面积是
某几何体的三视图如图所示,该几何体的表面积是