题目内容
已知函数f(x)=|x-2|+1,g(x)=kx.若方程f(x)=g(x)有两个不等实数根,则实数k的取值范围是 .
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:由题意作图,由临界值求实数k的取值范围.
解答:
 解:由题意,作图如图,
解:由题意,作图如图,
方程f(x)=g(x)有两个不等实数根可化为
函数f(x)=|x-2|+1与g(x)=kx的图象有两个不同的交点,
g(x)=kx表示过原点的直线,斜率为k,
如图,当过点(2,1)时,k=
,有一个交点,
当平行时,即k=1是,有一个交点,
结合图象可得,
<k<1;
故答案为:(
,1).
 解:由题意,作图如图,
解:由题意,作图如图,方程f(x)=g(x)有两个不等实数根可化为
函数f(x)=|x-2|+1与g(x)=kx的图象有两个不同的交点,
g(x)=kx表示过原点的直线,斜率为k,
如图,当过点(2,1)时,k=
| 1 |
| 2 |
当平行时,即k=1是,有一个交点,
结合图象可得,
| 1 |
| 2 |
故答案为:(
| 1 |
| 2 |
点评:本题考查了方程的根与函数的交点的关系,同时考查了函数的图象的应用,属于中档题.

练习册系列答案
相关题目
若函数f(x)=log2a-1(a2-2a+1)的值为正数,则a的取值范围是( )
| A、(0,2) | ||
B、(0,
| ||
| C、(-∞,0)∪(2,+∞) | ||
D、(
|
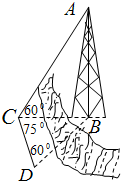 测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=75°,∠BDC=60°,CD=100m.并在点C测得塔顶A的仰角∠ACB=60°,求:塔高AB.
测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个侧点C与D.现测得∠BCD=75°,∠BDC=60°,CD=100m.并在点C测得塔顶A的仰角∠ACB=60°,求:塔高AB. 已知函数f(x)=
已知函数f(x)=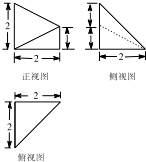 某几何体的三视图如图所示,该几何体的表面积是
某几何体的三视图如图所示,该几何体的表面积是