Question

已知函数f（x）=|x|+

m

x

-1（x≠0）
（1）若对任意x∈R，不等式f（2^x）＞0恒成立，求m的取值范围；
（2）讨论函数m²=3零点的个数．

Answer 1

考点：函数恒成立问题,根的存在性及根的个数判断

专题：函数的性质及应用,不等式的解法及应用

分析：（1）把不等式f（2^x）＞0转化为m＞2^x-（2^x）²，利用配方法求得2^x-（2^x）²的最大值得答案；
（2）由f（x）=0得x|x|-x+m=0（x≠0），变为m=-x|x|+x（x≠0），分别作出函数y=m和分段函数
g（x）=-x|x|+x（x≠0）的图象得答案．

解答： 解：（1）由f（2^x）＞0，得|2x|+

m

2x

-1＞0，
变形为（2^x）²-2^x+m＞0，即m＞2^x-（2^x）²，
而2x-(2x)2=-(2x-

1

2

)2+

1

4

，
当2x=

1

2

，即x=-1时，(2x-(2x)2)max=

1

4

，
∴m＞

1

4

；
（2）由f（x）=0，可得x|x|-x+m=0（x≠0），
变为m=-x|x|+x（x≠0），
令g(x)=x-x|x|=

-x2+x，x＞0 x2+x，x＜0

，
作y=g（x）的图象及直线y=m如图，

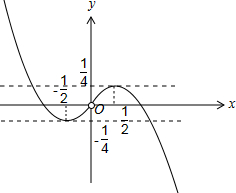
由图象可得：
当m＞

1

4

或m＜-

1

4

时，f（x）有1个零点．
当m=

1

4

或m=0或m=-

1

4

时，f（x）有2个零点．
当0＜m＜

1

4

或-

1

4

＜m＜0时，f（x）有3个零点．

点评：本题考查了函数恒成立问题，考查了利用配方法求函数的最值，体现了数形结合的解题思想方法，是中档题．