题目内容
两个等差数列{an},{bn},
=
,则
= .
| a1+a2+…+an |
| b1+b2+…+bn |
| 7n+2 |
| n+3 |
| an |
| bn |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:利用等差数列的通项性质,结合前n项和的公式,即可得出结论.
解答:
解:设等差数列{an},{bn}的前n项的和分别为Sn和Tn,则
=
=
=
=
.
故答案为:
.
| an |
| bn |
| ||
|
| S2n-1 |
| T2n-1 |
| 7(2n-1)+2 |
| (2n-1)+3 |
| 14n-5 |
| 2n+2 |
故答案为:
| 14n-5 |
| 2n+2 |
点评:考查学生灵活运用等差数列的通项公式及前n项和的公式化简求值,比较基础.

练习册系列答案
相关题目
已知x,y满足x+2y=2,那么3x+9y的最小值是( )
| A、3 | B、6 | C、9 | D、不存在 |
(B题)下列说法中正确的是( )
| A、任何三个不共线的向量可构成空间向量的一个基底 |
| B、空间的基底有且仅有一个 |
| C、两两垂直的三个非零向量可构成空间的一个基底 |
| D、基底{a,b,c}中基向量与基底{e,f,g}中基向量对应相等 |
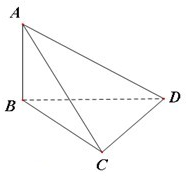 如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为
如图,AB⊥平面BCD,BD⊥CD,若AB=BC=2BD,则二面角B-AC-D的正弦值为