题目内容
定义在R上的偶函数f(x)在[0,+∞)上递增,且f(3m-1)>f(5),则m的范围是 .
考点:奇偶性与单调性的综合
专题:函数的性质及应用
分析:利用函数的奇偶性和单调性之间的关系将不等式转化为f(|3m-1|)>f(5),即可得到结论.
解答:
解:∵y=f(x)是定义在R上的偶函数,
∴不等式f(m)<f(1)等价为f(|3m-1|)>f(5),
∵函数f(x)在[0,+∞)上单调递增,
∴|3m-1|>5,
解得m>2或m<-
故答案为m>2或m<-
∴不等式f(m)<f(1)等价为f(|3m-1|)>f(5),
∵函数f(x)在[0,+∞)上单调递增,
∴|3m-1|>5,
解得m>2或m<-
| 4 |
| 3 |
故答案为m>2或m<-
| 4 |
| 3 |
点评:本题主要考查不等式的求解,利用函数的奇偶性和单调性之间的关系,将不等式进行转化是解决本题的关键,综合考查函数的性质.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
在△ABC中,sinA:sinB:sinC=3:5:7,则△ABC的最大内角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
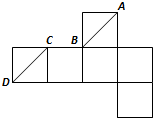 一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中成立的序号是
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中成立的序号是