题目内容
已知x1是方程x•10x=2013的根,x2是方程x•lgx=2013的根,则x1•x2= .
考点:根的存在性及根的个数判断
专题:计算题,作图题,函数的性质及应用
分析:将方程的根看成函数图象的交点,由图象特征求解.
解答:
解:如图,为y=
,y=10x,y=lgx的图象,
可知:点A的横坐标为x1,点B的横坐标为x2,
由图可知,A、B关于直线y=x对称,
又∵y=
关于直线y=x对称,
则x2=
;
则x1•x2=2013.
故答案为:2013.
| 2013 |
| x |

可知:点A的横坐标为x1,点B的横坐标为x2,
由图可知,A、B关于直线y=x对称,
又∵y=
| 2013 |
| x |
则x2=
| 2013 |
| x1 |
则x1•x2=2013.
故答案为:2013.
点评:本题考查了方程与函数的关系,同时考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
函数f(x)=x+
( )
| 2 |
| x |
| A、既不是奇函数,又不是偶函数 |
| B、既是奇函数,又是偶函数 |
| C、是偶函数,但不是奇函数 |
| D、是奇函数,但不是偶函数 |
已知函数f(x)是定义在R上的可导函数,且f(-1)=2,f′(x)>2,则不等式f(x)>2x+4的解集为( )
| A、(-∞,-1) |
| B、(-1,+∞) |
| C、(-1,0) |
| D、(0,+∞) |
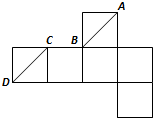 一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中成立的序号是
一个正方体的展开图如图所示,A、B、C、D为原正方体的顶点,则在原来的正方体中成立的序号是