题目内容
设函数f(x)=lnx-x2+ax(其中无理数e=2.71828…,a∈R).
(I)若函数f(x)的图象在x=
处的切线与直线y=2x平行,求实数a的值,并求此时函数f(x)的值域;
(Ⅱ)证明:?λ∈(0,1),?x1,x2∈(0,+∞),f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2);
(Ⅲ)设g(x)=xe1-x,若对于任意给定的x0∈(0,e],方程 f(x)+1=g(x0)在(0,e]内有两个不同的根,求实数a的取值范围.
(I)若函数f(x)的图象在x=
| 1 |
| 2 |
(Ⅱ)证明:?λ∈(0,1),?x1,x2∈(0,+∞),f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2);
(Ⅲ)设g(x)=xe1-x,若对于任意给定的x0∈(0,e],方程 f(x)+1=g(x0)在(0,e]内有两个不同的根,求实数a的取值范围.
考点:利用导数研究曲线上某点切线方程
专题:综合题,导数的综合应用
分析:(I)利用导数的几何意义,求出实数a的值,确定函数的单调性,可求函数f(x)的值域;
(Ⅱ)利用分析法进行证明,证明(1):[λx1+(1-λ)x2]2+[λx12+(1-λ)x22]=λ(1-λ)(x1-x2)2≥0;(2):ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]=ln
≥0即可;
(Ⅲ)求出函数g(x)在(0,e]上的值域为(0,1],令F(x)=f(x)+1,F′(x)=0在(0,e)有解,且易知只能有一个解,利用F(x)max=F(x0)>1,分离参数,即可得出结论.
(Ⅱ)利用分析法进行证明,证明(1):[λx1+(1-λ)x2]2+[λx12+(1-λ)x22]=λ(1-λ)(x1-x2)2≥0;(2):ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]=ln
λ(
| ||
(
|
(Ⅲ)求出函数g(x)在(0,e]上的值域为(0,1],令F(x)=f(x)+1,F′(x)=0在(0,e)有解,且易知只能有一个解,利用F(x)max=F(x0)>1,分离参数,即可得出结论.
解答:
(Ⅰ)解:∵f(x)=lnx-x2+ax,
∴f′(x)=
-2x+a,…(1分)
∵函数f(x)的图象在x=
处的切线与直线y=2x平行,
∴f′(
)=2,
解得a=1. …(2分)
此时f(x)=lnx-x2+x,f′(x)=
,
当x∈(0,1)时,f′(x)>0,f(x)为增函数;当x∈(1,+∞)时,f′(x)<0,f(x)为减函数.
由此可知,当x=1时f(x)取得极大值0(同时也是最大值).
∴函数f(x)的值域为(-∞,0].…(3分)
(Ⅱ)证明:要证:?λ∈(0,1),?x1,x2∈(0,+∞),f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),
只需要证明ln[(λx1+(1-λ)x2)]-[λx1+(1-λ)x2]2+a[λx1+(1-λ)x2]≥λ[lnx1-x12+ax1]+(1-λ)[lnx2-x22+ax2]即可.
也就是要证明ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]-[λx1+(1-λ)x2]2+[λx12+(1-λ)x22]≥0
∵(1):[λx1+(1-λ)x2]2+[λx12+(1-λ)x22]=λ(1-λ)(x1-x2)2≥0; …(5分)
(2):ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]=ln
下面证明
≥1,即要证明λ(
)+(1-λ)≥(
)λ,
不妨设0<x1≤x2,令t=
,h(t)=λt-tλ+(1-λ)(0<t≤1)
∴h′(t)=λ(1-tλ-1),
∵0<t≤1,0<λ<1,
∴h′(t)≤0,仅当t=1时h′(t)=0,
∴h(t)在(0,1]上是减函数,
∴h(t)≥h(1)=0,即ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]≥0.
结合(1),(2)可知(1)+(2)≥0,因此f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2);…(8分)
(Ⅲ)解:g′(x)=e1-x-xe1-x=(1-x)e1-x
当x∈(0,1)时,g′(x)>0,函数g(x)单调递增;
当x∈(1,e]时,g′(x)<0,函数g(x)单调递减.
∵g(0)=0,g(1)=1,g(e)=e•e1-e>0
∴函数g(x)在(0,e]上的值域为(0,1].…(9分)
令F(x)=f(x)+1,F′(x)=-
,
若F′(x)=0在(0,e]无解,则F(x)在(0,e]上是单调函数,不合题意;
∴F′(x)=0在(0,e)有解,且易知只能有一个解. …(10分)
设其解为x0,当x∈(0,x0)时F′(x)>0,F(x)在(0,x0)上是增函数;
当x∈(x0,e)时F′(x)<0,F(x)在(x0,e)上是减函数.
∵?x0∈(0,e],方程f(x)+1=g(x0)在(0,e]内有两个不同的根,
∴F(x)max=F(x0)>1,且F(e)≤0.
由F(e)≤0,即lne-e2+ae+1≤0,解得a≤e-
. …(11分)
由F(x)max=F(x0)>1,即lnx0-
+ax0>0.
∵2x02-ax0-1=0,∴a=2x0-
,
代入lnx0-
+ax0>0,得lnx0+x02-1>0.
设m(x)=lnx+x2-1,m′(x)=
+2x>0,∴m(x)在(0,e)上是增函数,
而m(1)=0,由lnx0+x02-1>0可得m(x0)>m(1),
得1<x0<e. …(12分)
由a=2x0-
是增函数,得1<a<2e-
. …(13分)
综上所述1<a≤e-
.…(14分)
∴f′(x)=
| 1 |
| x |
∵函数f(x)的图象在x=
| 1 |
| 2 |
∴f′(
| 1 |
| 2 |
解得a=1. …(2分)
此时f(x)=lnx-x2+x,f′(x)=
| (2x+1)(x-1) |
| x |
当x∈(0,1)时,f′(x)>0,f(x)为增函数;当x∈(1,+∞)时,f′(x)<0,f(x)为减函数.
由此可知,当x=1时f(x)取得极大值0(同时也是最大值).
∴函数f(x)的值域为(-∞,0].…(3分)
(Ⅱ)证明:要证:?λ∈(0,1),?x1,x2∈(0,+∞),f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2),
只需要证明ln[(λx1+(1-λ)x2)]-[λx1+(1-λ)x2]2+a[λx1+(1-λ)x2]≥λ[lnx1-x12+ax1]+(1-λ)[lnx2-x22+ax2]即可.
也就是要证明ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]-[λx1+(1-λ)x2]2+[λx12+(1-λ)x22]≥0
∵(1):[λx1+(1-λ)x2]2+[λx12+(1-λ)x22]=λ(1-λ)(x1-x2)2≥0; …(5分)
(2):ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]=ln
λ(
| ||
(
|
下面证明
λ(
| ||
(
|
| x1 |
| x2 |
| x1 |
| x2 |
不妨设0<x1≤x2,令t=
| x1 |
| x2 |
∴h′(t)=λ(1-tλ-1),
∵0<t≤1,0<λ<1,
∴h′(t)≤0,仅当t=1时h′(t)=0,
∴h(t)在(0,1]上是减函数,
∴h(t)≥h(1)=0,即ln[(λx1+(1-λ)x2)]-[λlnx1+(1-λ)lnx2]≥0.
结合(1),(2)可知(1)+(2)≥0,因此f(λx1+(1-λ)x2)≥λf(x1)+(1-λ)f(x2);…(8分)
(Ⅲ)解:g′(x)=e1-x-xe1-x=(1-x)e1-x
当x∈(0,1)时,g′(x)>0,函数g(x)单调递增;
当x∈(1,e]时,g′(x)<0,函数g(x)单调递减.
∵g(0)=0,g(1)=1,g(e)=e•e1-e>0
∴函数g(x)在(0,e]上的值域为(0,1].…(9分)
令F(x)=f(x)+1,F′(x)=-
| 2x2-ax-1 |
| x |
若F′(x)=0在(0,e]无解,则F(x)在(0,e]上是单调函数,不合题意;
∴F′(x)=0在(0,e)有解,且易知只能有一个解. …(10分)
设其解为x0,当x∈(0,x0)时F′(x)>0,F(x)在(0,x0)上是增函数;
当x∈(x0,e)时F′(x)<0,F(x)在(x0,e)上是减函数.
∵?x0∈(0,e],方程f(x)+1=g(x0)在(0,e]内有两个不同的根,
∴F(x)max=F(x0)>1,且F(e)≤0.
由F(e)≤0,即lne-e2+ae+1≤0,解得a≤e-
| 2 |
| e |
由F(x)max=F(x0)>1,即lnx0-
| x | 2 0 |
∵2x02-ax0-1=0,∴a=2x0-
| 1 |
| x0 |
代入lnx0-
| x | 2 0 |
设m(x)=lnx+x2-1,m′(x)=
| 1 |
| x |
而m(1)=0,由lnx0+x02-1>0可得m(x0)>m(1),
得1<x0<e. …(12分)
由a=2x0-
| 1 |
| x0 |
| 1 |
| e |
综上所述1<a≤e-
| 2 |
| e |
点评:本题主要考查了学生会利用导函数的正负确定函数的单调性,会根据函数的增减性求出闭区间上函数的最值,能够判断不等式恒成立时所满足的条件.难度大

练习册系列答案
相关题目
已知{a1,a2,a3,a4,a5}?{1,2,3,4,5,6},若a2>a1,a2>a3,a4>a3,a4>a5称排列a1a2a3a4a5为好排列,则好排列的个数为( )
| A、20 | B、72 | C、96 | D、120 |
“x<0”是“ln(x+1)<0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
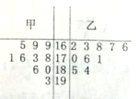 甲、乙两名工人生产的零件尺寸记成如图所示的茎叶图,已知零件尺寸在区间[165,180]内的为合格品.(单位:mm)
甲、乙两名工人生产的零件尺寸记成如图所示的茎叶图,已知零件尺寸在区间[165,180]内的为合格品.(单位:mm)