题目内容
已知圆G:x2+y2-2
x-2y=0经过椭圆
+
=1(a>b>0)的右焦点及上顶点.过椭圆外一点M(m,0)(m>a),倾斜角为
π的直线l交椭圆于C,D两点,若点N(3,0)在以线段CD为直径的圆E的外部,则m的取值范围是 .
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 3 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由圆的方程与坐标轴的交点得到椭圆的半焦距及半短轴长,结合a2=b2+c2求得半长轴长,可求椭圆的方程;设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,由判别式大于0求出m的初步范围,再设出交点坐标,由点N(3,0)在以线段CD为直径的圆E的外部,转化为
•
>0求解m的范围,最后取交集得答案.
| NC |
| ND |
解答:
解:∵圆G:x2+y2-2
x-2y=0与x轴、y轴交点为(2
,0),和(0,2),
∴c=2
,b=2,
∴a2=b2+c2=12,
∴椭圆方程为:
+
=1,
设直线l的方程为:y=-
(x-m),(m>2
)
由
可得:10x2-18mx+9m2-12=0.
由△=324m2-40(9m2-12)>0,
可得:-
<m<
,
设C(x1,y1),D(x2,y2),
x1+x2=
,x1•x2=
,
•
=(x1-3,y1)•(x2-3,y2)=(x1-3)(x2-3)+y1y2
=4x1x2-(3m+3)(x1+x2)+9+3m2>0.
化简得:2m2-9m+7>0,解得:m>
∴m的取值范围是(
,
),
故答案为:(
,
)
| 2 |
| 2 |
∴c=2
| 2 |
∴a2=b2+c2=12,
∴椭圆方程为:
| x2 |
| 12 |
| y2 |
| 4 |
设直线l的方程为:y=-
| 3 |
| 3 |
由
|
由△=324m2-40(9m2-12)>0,
可得:-
2
| ||
| 3 |
2
| ||
| 3 |
设C(x1,y1),D(x2,y2),
x1+x2=
| 9m |
| 5 |
| 9m2-12 |
| 10 |
| NC |
| ND |
=4x1x2-(3m+3)(x1+x2)+9+3m2>0.
化简得:2m2-9m+7>0,解得:m>
| 7 |
| 2 |
∴m的取值范围是(
| 7 |
| 2 |
2
| ||
| 3 |
故答案为:(
| 7 |
| 2 |
2
| ||
| 3 |
点评:本题考查了椭圆的标准方程,考查了直线与圆锥曲线的关系,体现了数学转化思想方法,训练了利用向量法求解与圆锥曲线有关的问题,“设而不求”的解题思想使问题的求解得到了简化,是高考试卷中的压轴题.

练习册系列答案
相关题目
将函数y=sin2x+
cos2x(x∈R)的图象向右平移m(m>0)个单位长度后,所得到的图象关于原点对称,则m的最小值为( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知an=3n+2,n∈N*,如果执行如图所示的程序框图,那么输出的S等于( )

| A、18.5 | B、37 |
| C、185 | D、370 |
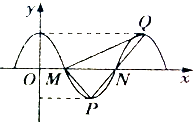 已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP=
已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP= 若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<
若如图框图所给程序运行的结果为S=360,那么判断框中应填入的关于k的判断条件是k<