题目内容
已知函数f(x)=lnx+a(2-x)
(Ⅰ)设曲线y=f(x)在点(1,f(1))处的切线为l,若l与圆(x-3)2+y2=1相切,求a的值;
(Ⅱ)讨论函数f(x)的单调性.
(Ⅰ)设曲线y=f(x)在点(1,f(1))处的切线为l,若l与圆(x-3)2+y2=1相切,求a的值;
(Ⅱ)讨论函数f(x)的单调性.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)求出切线方程,利用l与圆(x-3)2+y2=1相切,结合点到直线的距离公式,即可求a的值;
(Ⅱ)求导数,分类讨论,利用导数的正负,即可求出函数f(x)的单调性.
(Ⅱ)求导数,分类讨论,利用导数的正负,即可求出函数f(x)的单调性.
解答:
解:(Ⅰ)函数f(x)的定义域{x|x>0},f′(x)=
-a,
∴f′(1)=1-a
∴在(1,f(1))处的切线为:y-a=(1-a)(x-1),即(1-a)x-y-1+2a=0,
又已知圆的圆心为(3,0),半径为1,∴
=1,
解得a=1; …(7分)
(Ⅱ)函数f(x)的定义域{x|x>0},f′(x)=
-a,
当a≤0时,f′(x)=
-a>0恒成立,函数f(x)在(0,+∞)上单调递增
当a>0,令f′(x)>0解得0<x<
,令f′(x)<0解得x>
,
∴函数f(x)在区间(0,
)上单调递增,在区间(
,+∞)上单调递减 …(12分)
综上所述:当a≤0时,函数f(x)在(0,+∞)上单调递增;当a>0,函数f(x)在区间(0,
)上单调递增,在区间(
,+∞)上单调递减 …(13分)
| 1 |
| x |
∴f′(1)=1-a
∴在(1,f(1))处的切线为:y-a=(1-a)(x-1),即(1-a)x-y-1+2a=0,
又已知圆的圆心为(3,0),半径为1,∴
| |3(1-a)-1+2a| | ||
|
解得a=1; …(7分)
(Ⅱ)函数f(x)的定义域{x|x>0},f′(x)=
| 1 |
| x |
当a≤0时,f′(x)=
| 1 |
| x |
当a>0,令f′(x)>0解得0<x<
| 1 |
| a |
| 1 |
| a |
∴函数f(x)在区间(0,
| 1 |
| a |
| 1 |
| a |
综上所述:当a≤0时,函数f(x)在(0,+∞)上单调递增;当a>0,函数f(x)在区间(0,
| 1 |
| a |
| 1 |
| a |
点评:本题考查导数知识的综合运用,考查导数的几何意义,考查函数的单调性,正确求导是关键.

练习册系列答案
相关题目
若tanθ=
,则
=( )
| 3 |
| sin2θ |
| 1+cos2θ |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
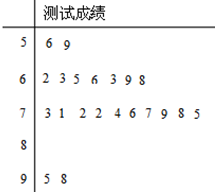 某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下:
某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下: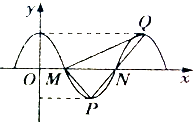 已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP=
已知函数f(x)=Acosωx(ω>0)的部分图象如图所示,且∠MQP=