题目内容
已知抛物线y2=2px(p>0)的焦点过F,过H(-
,0)引直线l交此抛物线于A,B两点.
(1)若直线AF的斜率为2,求直线BF的斜率;
(2)若p=2,点M在抛物线上,且
+
=t
,求t的取值范围.
| p |
| 2 |
(1)若直线AF的斜率为2,求直线BF的斜率;
(2)若p=2,点M在抛物线上,且
| FA |
| FB |
| FM |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程,圆锥曲线中的最值与范围问题
分析:(1)分别过A,B作准线的垂线,垂足分别是A1,B1可知AF=AA1,BF=BB1,进而根据
=
=
的比例关系,把边转换为角的正弦,求得sin∠AFH=sin∠BFH,进而根据∠AFH=180°-∠BFH=∠BFx,推断出kBF+kAF=0,求得答案..
(2)依题意可知,抛物线为y2=4x,直线l的斜率k存在且k≠0,l的方程为y=k(x+1),设交点A(x1,y1),B(x2,y2),联立方程消去y,根据△>0求得k的一个范围,利用韦达定理和已知向量的关系,求得M点的横坐标和纵坐标的表达式,进而组件k和t的关系式,利用k范围求得t的范围.
| AF |
| BF |
| AA1 |
| BB1 |
| HA |
| HB |
(2)依题意可知,抛物线为y2=4x,直线l的斜率k存在且k≠0,l的方程为y=k(x+1),设交点A(x1,y1),B(x2,y2),联立方程消去y,根据△>0求得k的一个范围,利用韦达定理和已知向量的关系,求得M点的横坐标和纵坐标的表达式,进而组件k和t的关系式,利用k范围求得t的范围.
解答:
解:(Ⅰ)分别过A,B作准线的垂线,垂足分别是A1,B1
则AF=AA1,BF=BB1,
∴
=
=
,
∴
=
,
∴
=
…①
△AHF中,
=
…②,
△BHF中,
=
…③
将②③代入①,得
=
,
∴sin∠AFH=sin∠BFH
∴∠AFH=180°-∠BFH=∠BFx,
∴kBF+kAF=0,
∴kBF=-kAF=-2.
(Ⅱ)依题意可知,抛物线为y2=4x,直线l的斜率k存在且k≠0,l的方程为y=k(x+1),设交点A(x1,y1),B(x2,y2),满足
,
即x1,x2满足k2x2+(2k2-4)x+k2=0,
∴△=(2k2-4)2-4k4>0,
∴k2<1,
且x1+x2=
,x1x2=1设M(x0,y0),由
+
=t
,其中t≠0,
得(x1-1,y1)+(x2-1,y2)=t(x0-1,y0),
∴
,
而y1+y2=k(x1+x2+2)=
,代入
=x0,得(
)2=4(
+1),
化为:k2t2-4k2t+4t=4得,k2=
,而k2<1,
且k≠0,
∴t<-2,或0<t<1,或1<t<2,或t>4.

则AF=AA1,BF=BB1,
∴
| AF |
| BF |
| AA1 |
| BB1 |
| HA |
| HB |
∴
| AF |
| BF |
| HA |
| HB |
∴
| AF |
| HA |
| BF |
| HB |
△AHF中,
| AF |
| HA |
| sin∠AHF |
| sin∠AFH |
△BHF中,
| BF |
| HB |
| sin∠AHF |
| sin∠BFH |
将②③代入①,得
| sin∠AHF |
| sin∠AFH |
| sin∠AHF |
| sin∠BFH |
∴sin∠AFH=sin∠BFH
∴∠AFH=180°-∠BFH=∠BFx,
∴kBF+kAF=0,
∴kBF=-kAF=-2.
(Ⅱ)依题意可知,抛物线为y2=4x,直线l的斜率k存在且k≠0,l的方程为y=k(x+1),设交点A(x1,y1),B(x2,y2),满足
|
即x1,x2满足k2x2+(2k2-4)x+k2=0,
∴△=(2k2-4)2-4k4>0,
∴k2<1,
且x1+x2=
| 4-2k2 |
| k2 |
| FB |
| FA |
| FM |
得(x1-1,y1)+(x2-1,y2)=t(x0-1,y0),
∴
|
而y1+y2=k(x1+x2+2)=
| 4 |
| k |
| y | 2 0 |
| 4 |
| kt |
| ||
| t |
化为:k2t2-4k2t+4t=4得,k2=
| 4-4t |
| t2-4t |
且k≠0,
∴t<-2,或0<t<1,或1<t<2,或t>4.
点评:本题主要考查了圆锥曲线的位置关系,难度偏高,在考试常作为压轴题,考查了学生分析问题和推理的能力.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
设复数z满足关系z•i=-1+
i,那么z等于( )
| 3 |
| 4 |
A、
| ||
B、-
| ||
C、-
| ||
D、
|
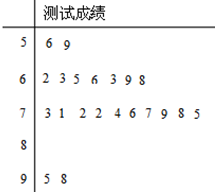 某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下:
某校高二一个班的一次地理测试中部分数据的茎叶图及频率分布表如下: