题目内容
19.已知$\vec a=({1,2}),\vec b=({-2,y})$,且$\vec a∥\vec b$.求:(Ⅰ)$\vec a•\vec b$;
(Ⅱ)$2\vec a-\vec b$.
分析 根据题意,若$\vec a∥\vec b$,由向量平行的坐标表示方法有1×y=2×(-2),解可得y的值,即可得$\overrightarrow{b}$的坐标,
(1)由向量数量积的坐标计算公式计算可得答案;
(2)由向量的坐标计算公式直接计算即可得答案.
解答 解:根据题意,已知$\vec a=({1,2}),\vec b=({-2,y})$,
若$\vec a∥\vec b$,则有1×y=2×(-2),即y=-4;
即$\overrightarrow{b}$=(-2,-4);
(1)$\overrightarrow{a}$•$\overrightarrow{b}$=1×(-2)+2×(-4)=-10;
(2)2$\overrightarrow{a}$-$\overrightarrow{b}$=(2,4)-(-2,-4)=(4,8).
点评 本题考查向量的坐标计算,关键要掌握向量的坐标计算以及数量积的计算公式.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
7.若点(x,y)在圆$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}\right.$(θ为参数)上,则x2+y2的最小值是9.
14.已知$|{\vec b}|=3$,$\vec a$在$\vec b$方向上的投影为$\frac{3}{2}$,则$\vec a$•$\vec b$=( )
| A. | 2 | B. | $\frac{9}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
 20名学生某次数学成绩(单位:分)的频率分布直方图如图:
20名学生某次数学成绩(单位:分)的频率分布直方图如图: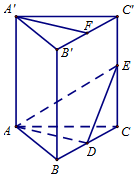 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证: