题目内容
4.二次函数f(x)=7x2-(m+13)x-m-2(m∈R)的两个零点分别分布在区间(0,1)和(1,2)内,则实数m的取值范围为(-4,-2).分析 由函数零点的判定定理列出不等式组,求得实数m的取值范围.
解答 解:由题意可知:二次函数f(x)=7x2-(m+13)x-m-2(m∈R)的两个零点
分别在区间(0,1)和(1,2),
$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\\{f(2)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{-m-2>0}\\{-2m-8<0}\\{-3m>0}\end{array}\right.$,解得:-4<m<-2,
∴实数m的取值范围(-4,-2),
故答案为:(-4,-2).
点评 本题考查一元二次函数零点的判定,考查不等式的解法,属于基础题.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.某地区2007年至2013年农村居民家庭人均纯收入y(单位:千元)的数据如表:
(1)求y关于t的线性回归方程;
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
可用公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n(\overline x{)^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{({x_i}-\overline x{)^2}}}}$,$\widehat{a}$=$\overline y$-$\widehat{b}$$\overline x$.
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(2)利用(1)中的回归方程,分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况,并预测该地区2015年农村居民家庭人均纯收入.
可用公式:$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n(\overline x{)^2}}}}$=$\frac{{\sum_{i=1}^n{({x_i}-\overline x)({y_i}-\overline y)}}}{{\sum_{i=1}^n{({x_i}-\overline x{)^2}}}}$,$\widehat{a}$=$\overline y$-$\widehat{b}$$\overline x$.
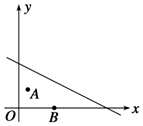 如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方?
如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方? 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.