题目内容
9. 20名学生某次数学成绩(单位:分)的频率分布直方图如图:
20名学生某次数学成绩(单位:分)的频率分布直方图如图:(Ⅰ)求a的值,并估计这20名学生的平均成绩;
(Ⅱ)从这20名同学中任选3人参加某项活动,求恰好有1人的成绩在[50,70)中的概率.
分析 (Ⅰ)由频率分布直方图的性质能求出$a=\frac{1}{400}$,由此能估计这20名学生的平均成绩.
(Ⅱ)由[50,70)的学生有2人,记恰好有1人的成绩在[50,70)中为事件A,利用排列组合知识能求出恰好有1人的成绩在[50,70)中的概率.
解答 解:(Ⅰ)由频率分布直方图的性质得:
(2a+3a+7a+6a+2a)×20=20a×20=1,得$a=\frac{1}{400}$,
$\overline x=2a×20×60+3a×20×80+7a×20×100+6a×20×120+2a×20×140$=41200a=103(分). …(6分)
(Ⅱ)由(Ⅰ)可知,[50,70)的学生有2人,…(8分)
记恰好有1人的成绩在[50,70)中为事件A,
则$P(A)=\frac{{C_2^1•C_{18}^2}}{{C_{20}^3}}=\frac{{2×\frac{17×18}{2}}}{{\frac{18×19×20}{3×2}}}=\frac{51}{190}$.
所以,恰好有1人的成绩在[50,70)中的概率是$\frac{51}{190}$. …(12分)
点评 本题考查频率分布直方图的求法,考查概率的求法,是基础题,解题时要认真审题,注意频率分布直方图的性质、等可能事件概率加法公式的合理运用.

练习册系列答案
相关题目
20.设m,n是平面α内的两条不同直线,l1,l2是平面β内的两条相交直线,则以下能够推出α∥β的是( )
| A. | m∥β且l1∥α | B. | m∥l1且n∥l2 | C. | m∥β且n∥β | D. | m∥β且n∥l2 |
17.已知函数f(x)=exlnx(x>0),若对$?x∈[{\frac{1}{e},e}],?k∈[{-a,a}]({a>0})$使得方程f(x)=k有解,则实数a的取值范围是( )
| A. | (0,ee] | B. | [ee,+∞) | C. | [e,+∞) | D. | $[{{e^{\frac{1}{e}}},{e^e}}]$ |
4.给出如下列联表(公式见卷首)
参照公式,得到的正确结论是( )
| 患心脏病 | 患其它病 | 合 计 | |
| 高血压 | 20 | 10 | 30 |
| 不高血压 | 30 | 50 | 80 |
| 合 计 | 50 | 60 | 110 |
| A. | 有99%以上的把握认为“高血压与患心脏病无关” | |
| B. | 有99%以上的把握认为“高血压与患心脏病有关” | |
| C. | 在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病无关” | |
| D. | 在犯错误的概率不超过0.1%的前提下,认为“高血压与患心脏病有关” |
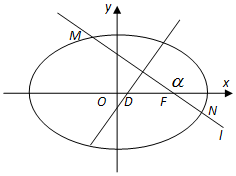 已知椭圆E的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),E上动点P到右焦点F距离的最大值为3,且离心率e=$\frac{1}{2}$.
已知椭圆E的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),E上动点P到右焦点F距离的最大值为3,且离心率e=$\frac{1}{2}$.