题目内容
11.已知集合A={x|1≤x≤2},B={x|m≤x≤m+3}.(1)当m=2时,求A∪B;
(2)若A⊆B,求实数m的取值范围.
分析 (1)m=2时,可以求出集合B,然后进行并集的运算即可;
(2)根据A⊆B便可得出$\left\{\begin{array}{l}{m≤1}\\{m+3≥2}\end{array}\right.$,解该不等式组即可得出实数m的取值范围.
解答 解:(1)当m=2时,B={x|2≤x≤5};
∴A∪B={x|1≤x≤2}∪{x|2≤x≤5}={x|1≤x≤5};
(2)∵A⊆B;
∴$\left\{{\begin{array}{l}{m≤1}\\{m+3≥2}\end{array}}\right.$;
解得-1≤m≤1;
∴实数m的取值范围为[-1,1].
点评 考查描述法表示集合的概念,并集的运算,以及子集的概念.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
2.否定“至多有两个解”的说法中,正确的是( )
| A. | 恰好有两个解 | B. | 至少有一个解 | C. | 至少有两个解 | D. | 至少有三个解 |
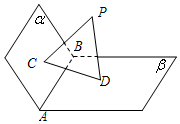 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.