题目内容
设函数f(x)=3sin(ωx+φ)(ω>0,-
<φ<
)的图象关于直线x=
对称,它的周期是π,则以下结论正确的个数( )
(1)f(x)的图象过点(0,
)
(2)f(x)的一个对称中心是(
,0)
(3)f(x)在[
,
]上是减函数
(4)将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象.
| π |
| 2 |
| π |
| 2 |
| 2π |
| 3 |
(1)f(x)的图象过点(0,
| 1 |
| 2 |
(2)f(x)的一个对称中心是(
| 5π |
| 12 |
(3)f(x)在[
| π |
| 12 |
| 2π |
| 3 |
(4)将f(x)的图象向右平移|φ|个单位得到函数y=3sinωx的图象.
| A、4 | B、3 | C、2 | D、1 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:由函数的周期求出ω,再由图象关于直线x=
对称结合φ的范围求得φ,则函数解析式可求.
①求得f(0)=
说明命题①错误;
②由f(
)=0说明命题②正确;
③求出原函数的减区间,由[
,
]是一个减区间的子集说明命题③正确;
④通y=Asin(ωx+φ)图象的平移说明命题④错误.
| 2π |
| 3 |
①求得f(0)=
| 3 |
| 2 |
②由f(
| 5π |
| 12 |
③求出原函数的减区间,由[
| π |
| 12 |
| 2π |
| 3 |
④通y=Asin(ωx+φ)图象的平移说明命题④错误.
解答:
解:∵f(x)=3sin(ωx+φ)(ω>0,-
<φ<
)的周期是π,
∴ω=2,
又图象关于直线x=
对称,则2×
+φ=kπ+
,即φ=kπ-
,k∈Z.
∵-
<φ<
,
∴取k=1得φ=
.
∴f(x)=3sin(2x+
).
①∵f(0)=3sin
=
.
∴f(x)的图象过点(0,
)错误;
②∵f(
)=3sin(2×
+
)=3sinπ=0.
∴f(x)的一个对称中心是(
,0)正确;
③由
+2kπ≤2x+
≤
+2kπ,得:
+kπ≤x≤
+kπ,k∈Z.
取k=0,得
≤x≤
.
∵[
,
]⊆[
,
],
∴f(x)在[
,
]上是减函数正确;
④∵φ=
>0,
∴f(x)=3sin(ωx+φ)=3sinω(x+
)是把y=3sinωx
向左平移
个单位得到,
则f(x)的图象向右平移
个单位得到函数y=3sinωx的图象.
∴命题④错误.
| π |
| 2 |
| π |
| 2 |
∴ω=2,
又图象关于直线x=
| 2π |
| 3 |
| 2π |
| 3 |
| π |
| 2 |
| 5π |
| 6 |
∵-
| π |
| 2 |
| π |
| 2 |
∴取k=1得φ=
| π |
| 6 |
∴f(x)=3sin(2x+
| π |
| 6 |
①∵f(0)=3sin
| π |
| 6 |
| 3 |
| 2 |
∴f(x)的图象过点(0,
| 1 |
| 2 |
②∵f(
| 5π |
| 12 |
| 5π |
| 12 |
| π |
| 6 |
∴f(x)的一个对称中心是(
| 5π |
| 12 |
③由
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
取k=0,得
| π |
| 6 |
| 2π |
| 3 |
∵[
| π |
| 12 |
| 2π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
∴f(x)在[
| π |
| 12 |
| 2π |
| 3 |
④∵φ=
| π |
| 6 |
∴f(x)=3sin(ωx+φ)=3sinω(x+
| φ |
| ω |
向左平移
| φ |
| ω |
则f(x)的图象向右平移
| φ |
| ω |
∴命题④错误.
点评:本题考查命题的真假判断与应用,考查了y=Asin(ωx+φ)型函数的图象和性质,训练了复合函数的单调性的求法,是中档题.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
曲线y=cosx(0≤x≤
π)与x轴以及直线x=
所围图形的面积为( )
| 3 |
| 2 |
| 3π |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
| D、3 |
直线y=5与y=-1在区间[0,π]上截曲线y=Asin2x+B(A>0,B>0)所得的线段长相等且不为0,则下列描述正确的是( )
A、A≤
| ||||
| B、A≤3,B=2 | ||||
C、A>
| ||||
| D、A>3,B=2 |
下列函数,在其定义域内既是奇函数又是增函数的是( )
| A、y=2x(x∈R) | ||
| B、y=-log2x(x>0,x∈R) | ||
| C、y=x+x3(x∈R) | ||
D、y=-
|
在(x+y)n的展开式中,若第九项系数最大,则n的值可能等于( )
| A、14,15 |
| B、15,16 |
| C、16,17 |
| D、14,15,16 |
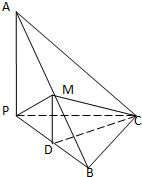 如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.