题目内容
18.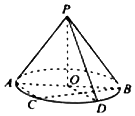 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.(Ⅰ)若弧$\widehat{BC}$的中点为D,求证:AC∥平面POD
(Ⅱ)如果△PAB面积是9,求此圆锥的表面积与体积.
分析 (Ⅰ)由AB是底面圆的直径,可得AC⊥BC.再由$\widehat{BC}$的中点为D,可得OD⊥BC.则AC∥OD.由线面平行的判定可得AC∥平面POD;
(Ⅱ)设圆锥底面圆半径为r,高为h,母线长为l,由题意可得h=r,l=$\sqrt{2}r$,由△PAB面积是9求得r=3,代入圆锥表面积公式与体积公式求解.
解答 (Ⅰ)证明:∵AB是底面圆的直径,∴AC⊥BC.
∵$\widehat{BC}$的中点为D,∴OD⊥BC.
又AC、OD共面,∴AC∥OD.
又AC?平面POD,OD?平面POD,
∴AC∥平面POD;
(Ⅱ)解:设圆锥底面圆半径为r,高为h,母线长为l,
∵圆锥的轴截面PAB为等腰直角三角形,∴h=r,l=$\sqrt{2}r$,
由${S}_{△ABP}=\frac{1}{2}×2r×h={r}^{2}=9$,得r=3,
∴${S}_{表面积}=πrl+π{r}^{2}=πr×\sqrt{2}r+π{r}^{2}=9(1+\sqrt{2})π$,
$V=\frac{1}{3}π{r}^{2}h=9π$.
点评 本题考查直线与平面平行的判定,考查圆锥表面积与体积的求法,考查空间想象能力,是中档题.

练习册系列答案
相关题目
9.若复数z满足(1+i)z=|$\sqrt{3}$+i|,则在复平面内,z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.已经等差数列{an}的前n项和为Sn,S9>0,S8<0,则使得Sn取得最小值的n为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
3.函数f(x)是定义在(-∞,+∞)内的可导函数,且满足:xf'(x)+f(x)>0,对于任意的正实数a,b,若a>b,则必有( )
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
8.已知$\frac{π}{2}<A<π$,且sinA=$\frac{4}{5}$,那么sin2A等于( )
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{12}{25}$ | D. | $-\frac{24}{25}$ |
 在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.