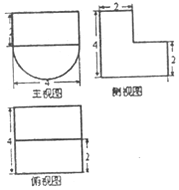
题目内容
8.已知$\frac{π}{2}<A<π$,且sinA=$\frac{4}{5}$,那么sin2A等于( )| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{12}{25}$ | D. | $-\frac{24}{25}$ |
分析 利用同角三角函数的基本关系,二倍角公式,求得sin2A的值.
解答 解:∵$\frac{π}{2}<A<π$,且sinA=$\frac{4}{5}$,∴cosA=-$\sqrt{{1-sin}^{2}A}$=-$\frac{3}{5}$,
∴sin2A=2sinAcosA=-$\frac{24}{25}$,
故选:D.
点评 本题主要考查同角三角函数的基本关系、二倍角公式的应用,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
3.函数y=lg(sin2x)+$\sqrt{9-{x^2}}$的定义域是( )
| A. | [-3,3] | B. | (0,$\frac{π}{2}$) | C. | [-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$) | D. | (-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$) |
20.已知数列{an}满足a1=0,an+1=an+2n,那么a2009的值是( )
| A. | 2 008×2009 | B. | 2008×2007 | C. | 2009×2 010 | D. | 20092 |
5.已知F1、F2分别为双曲线C:$\frac{x^2}{4}-\frac{y^2}{5}$=1的左、右焦点,P为双曲线C右支上一点,且|PF1|=2|PF2|,则△PF1F2外接圆的面积为( )
| A. | $\frac{4π}{15}$ | B. | $\frac{16π}{15}$ | C. | $\frac{64π}{15}$ | D. | $\frac{256π}{15}$ |
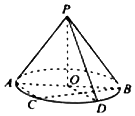 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.