题目内容

6．已经等差数列{an}的前n项和为Sn，S9＞0，S8＜0，则使得Sn取得最小值的n为（　　）
A．3B．4C．5D．6

分析 等差数列{an}的前n项和为Sn，S9＞0，S8＜0，利用求和公式及其性质可得：a5＞0，a4＜0，即可得出．

解答 解：∵等差数列{an}的前n项和为Sn，S9＞0，S8＜0，
∴$\frac{9（{a}_{1}+{a}_{9}）}{2}$=9a5＞0，$\frac{8（{a}_{1}+{a}_{8}）}{2}$=4（a5+a4）＜0，
解得a5＞0，a4＜0，
则使得Sn取得最小值的n为4．
故选：B．

点评 本题考查了等差数列的性质及其通项公式求和公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
16．用数学归纳法证明1+3+5+…+（2n-1）=n2（n∈n*）
17．已知tanα=2
（1）求$\frac{3sinα-2cosα}{sinα-cosα}$的值；
（2）若α是第三象限角，求cosα的值．
14．设a，b，c，d为正数，且a+b+c+d=1．证明：
（1）${a^2}+{b^2}+{c^2}+{d^2}≥\frac{1}{4}$；
（2）$\frac{a^2}{b}+\frac{b^2}{c}+\frac{c^2}{d}+\frac{d^2}{a}≥1$．
1．设等差数列{an}的前n项为Sn，已知S13＞0，S14＜0，若ak•ak+1＜0，则k=（　　）
A．6B．7C．13D．14
11．已知直线l1上的点满足ax+4y+6=0，直线l2上的点满足（$\frac{3}{4}$a+1）x+ay-$\frac{3}{2}$=0．试求：
（Ⅰ）a为何值时l1∥l2
（Ⅱ）a为何值时l1⊥l2．
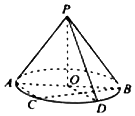18．如图，O是圆锥底面圆的圆心，圆锥的轴截面PAB为等腰直角三角形，C为底面圆周上一点．
（Ⅰ）若弧$\widehat{BC}$的中点为D，求证：AC∥平面POD
（Ⅱ）如果△PAB面积是9，求此圆锥的表面积与体积．
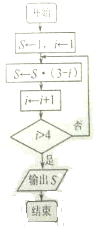15．阅读如图所示的程序框图，运行相应的程序，则输出S的值是0．
16．已知集合A={-1，0，1}，B={-2，-1，0，1，2}，现从集合A，B中各任取一个数．
（1）求这两数之和为0的概率；
（2）若从集合A，B中取出的数分别记为a，b，求方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$只有一个解的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网