题目内容
10.在△ABC中,A=50°,AB=2,且△ABC的面积为$\frac{{\sqrt{3}}}{2}$,则BC的长为$\sqrt{4+\frac{3}{4si{n}^{2}50}-\frac{2\sqrt{3}cos50°}{sin50°}}$.分析 根据三角形的面积公式,代入题中数据算出AC,再根据余弦定理加以计算,可得BC的值.
解答 解:∵A=50°,AB=2,
∴△ABC的面积为S=$\frac{1}{2}$•AB•AC•sin50°=$\frac{1}{2}×2×AC×sin50°$=$\frac{\sqrt{3}}{2}$,解得:AC=$\frac{\sqrt{3}}{2sin50°}$,
根据余弦定理,得
BC2=AB2+AC2-2AB•ACcosA=4+($\frac{\sqrt{3}}{2sin50°}$)2-2×2×$\frac{\sqrt{3}}{2sin50°}$×cos50°=4+$\frac{3}{4si{n}^{2}50°}$-$\frac{2\sqrt{3}cos50°}{sin50°}$,
∴BC=$\sqrt{4+\frac{3}{4si{n}^{2}50}-\frac{2\sqrt{3}cos50°}{sin50°}}$.
故答案为:$\sqrt{4+\frac{3}{4si{n}^{2}50}-\frac{2\sqrt{3}cos50°}{sin50°}}$.
点评 本题给出三角形的一边、一角,在已知面积的情况下求另一边长.着重考查了余弦定理、三角形的面积公式等知识,属于基础题.

练习册系列答案
相关题目
20.合肥一中高一年级开展研学旅行活动,高一1、2、3、4、5五个班级,分别从西安、扬州、皖南这三条线路中选一条开展研学活动,每条路线至少有一个班参加,且1、2两个班级不选同一条线路,则共有( )种不同的选法.
| A. | 72 | B. | 108 | C. | 114 | D. | 124 |
1.设等差数列{an}的前n项为Sn,已知S13>0,S14<0,若ak•ak+1<0,则k=( )
| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
20.已知数列{an}满足a1=0,an+1=an+2n,那么a2009的值是( )
| A. | 2 008×2009 | B. | 2008×2007 | C. | 2009×2 010 | D. | 20092 |
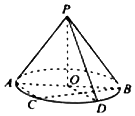 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.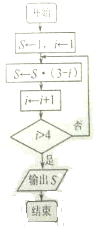 阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.
阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.