题目内容
13. 在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜
在海岸A处,发现北偏东45°方向,距离A为$(\sqrt{3}-1)$海里的B处有一艘走私船,在A处北偏西75°方向,距离A为2 海里的C处有一艘缉私艇奉命以$10\sqrt{3}$海里/时的速度追截走私船,此时,走私船正以10 海里/时的速度从B处向北偏东30°方向逃窜(Ⅰ)问C船与B船相距多少海里?C船在B船的什么方向?
(Ⅱ)问缉私艇沿什么方向行驶才能最快追上走私船?并求出所需时间.
分析 (I)在△ABC中根据余弦定理计算BC,再利用正弦定理计算∠ABC即可得出方位;
(II)在△BCD中,利用正弦定理计算∠BCD,再计算BD得出追击时间.
解答 解:(I)由题意可知AB=$\sqrt{3}$-1,AC=2,∠BAC=120°,
在△ABC中,由余弦定理得:BC2=AB2+AC2-2AB•AC•cos120°=6,
∴BC=$\sqrt{6}$.
由正弦定理得:$\frac{AC}{sin∠ABC}=\frac{BC}{sin∠BAC}$,即$\frac{2}{sin∠ABC}=\frac{\sqrt{6}}{\frac{\sqrt{3}}{2}}$,解得sin∠ABC=$\frac{\sqrt{2}}{2}$,
∴∠ABC=45°,
∴C船在B船的正西方向.
(II)由(1)知BC=$\sqrt{6}$,∠DBC=120°,设t小时后缉私艇在D处追上走私船,
则BD=10t,CD=10$\sqrt{3}$t,
在△BCD中,由正弦定理得:$\frac{10\sqrt{3}t}{sin120°}=\frac{10t}{sin∠BCD}$,
解得sin∠BCD=$\frac{1}{2}$,∴∠BCD=30°,
∴△BCD是等腰三角形,∴10t=$\sqrt{6}$,即t=$\frac{\sqrt{6}}{10}$.
∴缉私艇沿东偏北30°方向行驶$\frac{\sqrt{6}}{10}$小时才能最快追上走私船.
点评 本题考查了正余弦定理解三角形,解三角形的实际应用,属于中档题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
4.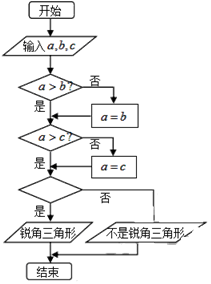 如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )
如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )
 如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )
如图程序框图中,若输入互不相等的三个正实数a,b,c,要求判断△ABC的形状,则空白的判断框中应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
1.设等差数列{an}的前n项为Sn,已知S13>0,S14<0,若ak•ak+1<0,则k=( )
| A. | 6 | B. | 7 | C. | 13 | D. | 14 |
8.若直线过点(1,2),(4,2+$\sqrt{3}$)则此直线的倾斜角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
3.函数y=lg(sin2x)+$\sqrt{9-{x^2}}$的定义域是( )
| A. | [-3,3] | B. | (0,$\frac{π}{2}$) | C. | [-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$) | D. | (-3,-$\frac{π}{2}$)∪(0,$\frac{π}{2}$) |
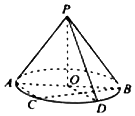 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.