题目内容
3.函数f(x)是定义在(-∞,+∞)内的可导函数,且满足:xf'(x)+f(x)>0,对于任意的正实数a,b,若a>b,则必有( )| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |
分析 构造g(x)=xf(x),利用其单调性逐一判断四个答案的正误,即可得出结论.
解答 解:令g(x)=xf(x),
则g′(x)=xf′(x)+f(x)>0,
∴函数g(x)在R上单调递增,
∵a>b,
∴g(a)>g(b),
∴af(a)>bf(b),
故选:D.
点评 正确构造g(x)=xf(x)和熟练掌握利用导数研究函数的单调性是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
12.若i是虚数单位,则复数$z=\frac{{1-\sqrt{3}i}}{2i}$在复平面内所对应的点位于( )
| A. | 第四象限 | B. | 第三象限 | C. | 第二象限 | D. | 第一象限 |
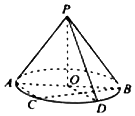 如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.
如图,O是圆锥底面圆的圆心,圆锥的轴截面PAB为等腰直角三角形,C为底面圆周上一点.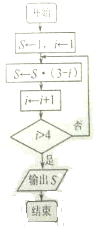 阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.
阅读如图所示的程序框图,运行相应的程序,则输出S的值是0.