题目内容
定义域为R的函数f(x)满足f(x+2)=2f(x),当x∈[0,2)时,f(x)=
则当x∈[-4,-2)时,函数f(x)的最小值为( )
|
A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
考点:分段函数的应用
专题:函数的性质及应用
分析:由条件f(x+2)=2f(x)推出f(x+4)=2f(x+2)=4f(x),即f(x)=
f(x+4),再分当-4≤x<-3与当-3≤x<-2两种情况,带入分段函数分别求出最小值.
| 1 |
| 4 |
解答:
解:∵f(x+2)=2f(x),∴f(x+4)=2f(x+2)=4f(x),即f(x)=
f(x+4),
由-4≤x<-2,得0≤x+4<2,
当-4≤x<-3时,0≤x+4<1,∴f(x)=
f(x+4)=
[(x+4)2-(x-4)],由于对称轴x+4=
,故当x+4=
时,f(x)min=
[(
)2-
]=-
;
当-3≤x<-2时,1≤x+4<2,∴f(x)=
f(x+4)=-
(
)|x+4-
|=-
(
)|x+
|,
由于复合函数y=-
(
)t为增函数,又|x+
|≥0,故当x+
=0时,f(x)min=-
(
)0=-
;
综上f(x)取最小值-
,
故选:B.
| 1 |
| 4 |
由-4≤x<-2,得0≤x+4<2,
当-4≤x<-3时,0≤x+4<1,∴f(x)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
当-3≤x<-2时,1≤x+4<2,∴f(x)=
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 2 |
由于复合函数y=-
| 1 |
| 4 |
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
综上f(x)取最小值-
| 1 |
| 4 |
故选:B.
点评:本题考查分段函数的应用,考查函数的最值及运用,同时考察二次函数、复合函数求最值,计算应细心.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
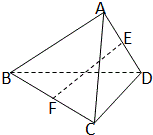 如图,在四面体ABCD中,E、F分别是AD、BC中,AB=CD=2,EF=
如图,在四面体ABCD中,E、F分别是AD、BC中,AB=CD=2,EF=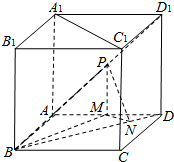 如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N. 如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
如图所示,圆O的两弦AB和CD交于点E,EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.