题目内容
已知△ABC中满足A-C=90°,a+c=
b,求角C.
| 2 |
考点:正弦定理的应用
专题:解三角形
分析:根据已知和正弦定理可得sinA+sinC=
sinB,由角的关系和范围可得sin2C=
,或-1,根据已知可求得角C的值.
| 2 |
| 1 |
| 2 |
解答:
解:∵A-C=90°,A+B+C=π,
∴A=90°+C,B=90°-2C,
∵a+c=
b,
∴由正弦定理可得sinA+sinC=
sinB,
∴sin(90°+C)+sinC=
sin(90°-2C),整理可得cosC+sinC=
cos2C
∴两边平方可得:1+sin2C=2cos22C=2-2sin22C,即有2sin22C+sin2C-1=0,从而可解得sin2C=
,或-1
∵0<C<90°,0<2C<180°
∴sin2C=
,有2C=
或
,
∴C=
或
(舍去).
∴C=
.
∴A=90°+C,B=90°-2C,
∵a+c=
| 2 |
∴由正弦定理可得sinA+sinC=
| 2 |
∴sin(90°+C)+sinC=
| 2 |
| 2 |
∴两边平方可得:1+sin2C=2cos22C=2-2sin22C,即有2sin22C+sin2C-1=0,从而可解得sin2C=
| 1 |
| 2 |
∵0<C<90°,0<2C<180°
∴sin2C=
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
∴C=
| π |
| 12 |
| 5π |
| 12 |
∴C=
| π |
| 12 |
点评:本题主要考查了正弦定理的应用,属于基本知识的考查.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
 已知四面体O-ABC中,M、N分别是OA、BC的中点,P是MN上(靠近点M)的三等分点,其中OA=OB=OC=1,∠AOC=∠AOB=∠BOC=60°,求异面直线OP与AB所成角的余弦值.(用向量法)
已知四面体O-ABC中,M、N分别是OA、BC的中点,P是MN上(靠近点M)的三等分点,其中OA=OB=OC=1,∠AOC=∠AOB=∠BOC=60°,求异面直线OP与AB所成角的余弦值.(用向量法)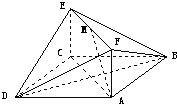 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=