题目内容
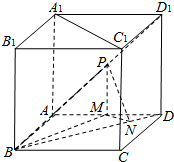 如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.
如图,正方体ABCD-A1B1C1D1的棱长为2,点P为面ADD1A1的对角线AD1的中点.PM⊥平面ABCD交AD与M,MN⊥BD于N.(1)求异面直线PN与A1C1所成角的大小;(结果可用反三角函数值表示)
(2)求三棱锥P-BMN的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离,空间角
分析:(1)判断出∠PNM为异面直线PN与A1C1所成角,在△PMN中,∠PMN为直角,tan∠PNM=
,求解得出异面直线PN与A1C1所成角的大小为arctan
.
(2)BN=
,运用VP-BMN=
•
•PM•MN•BN,求解得出体积.
| 2 |
| 2 |
(2)BN=
3
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
解答:
解:(1)∵点P为面ADD1A1的对角线AD1的中点,且PM⊥平面ABCD,
∴PM为△ADD1的中位线,得PM=1,
又∵MN⊥BD,
∴MN=ND=
MD=
,
∵在底面ABCD中,MN⊥BD,AC⊥BD,
∴MN∥AC,
又∵A1C1∥AC,∠PNM为异面直线PN与A1C1所成角,
在△PMN中,∠PMN为直角,tan∠PNM=
,
∴∠PNM=arctan
.
即异面直线PN与A1C1所成角的大小为arctan
.
(2)BN=2
-
=
,VP-BMN=
•
•PM•MN•BN,
代入数据得三棱锥P-BMN的体积为
.
∴PM为△ADD1的中位线,得PM=1,
又∵MN⊥BD,
∴MN=ND=
| ||
| 2 |
| ||
| 2 |
∵在底面ABCD中,MN⊥BD,AC⊥BD,
∴MN∥AC,
又∵A1C1∥AC,∠PNM为异面直线PN与A1C1所成角,
在△PMN中,∠PMN为直角,tan∠PNM=
| 2 |
∴∠PNM=arctan
| 2 |
即异面直线PN与A1C1所成角的大小为arctan
| 2 |
(2)BN=2
| 2 |
| ||
| 2 |
3
| ||
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
代入数据得三棱锥P-BMN的体积为
| 1 |
| 4 |
点评:本题考查了空间直线的夹角问题,空间几何体的体积计算,属于中档题.

练习册系列答案
相关题目
 抛物线的顶点在原点,焦点在x轴上,准线l与x轴相交于点A(-1,0),过点A的直线与抛物线相交于P、Q两点.
抛物线的顶点在原点,焦点在x轴上,准线l与x轴相交于点A(-1,0),过点A的直线与抛物线相交于P、Q两点. 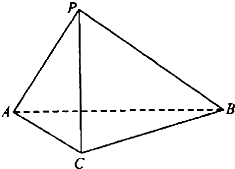 如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.