题目内容

用二分法求方程x3-2=0的近似值（精度为0.1）
考点：二分法求方程的近似解
专题：函数的性质及应用
分析：令f（x）=x3-2，因为f（1）=-1＜0，f（2）=6＞0，所以方程x3-2=0在区间[1，2]上有实数解，再根据用二分法求方程的近似解的方法和步骤，求得方程x3-2=0的近似解，即为所求．
解答： 解：本题即求函数f（x）=x3-2的一个正零点，
因为f（1）=-1＜0，f（2）=6＞0，所以方程x3-2=0在区间（1，2）上有实数解．
再根据f（1.5）=1.375＞0，f（1.5）•f（1）＜0，所以方程x3-2=0在区间（1，1.5）上有实数解．
…如此不断进行下去，得x3-2=0的实数解所在表如下：
 左端点右端点
112
211.5
31.251.5
41.251.375
51.251.3125
61.251.28125
得到方程x3-2=0的近似解为1.3．
点评：本题主要考查用二分法求方程的近似解的方法和步骤，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
已知y=2sin（2x-
π
3
），x∈[0，
π
6
]，求最值．
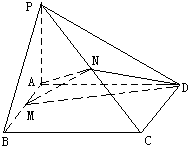已知：ABCD是矩形，设PA=a，PA⊥平面ABCD，M，N分别是AB，PC的中心点．
（1）若PA=BC，求证：MN⊥平面PCD；
（2）若PD=AB，且平面MND⊥平面PCD，求二面角P-CD-A的大小．
在数列{an}，{bn}中a1=2，an=an-1+2n，且an，bn，an+1成等差数列．
（1）求{an}，{bn}的通项公式；
（2）证明：
1
a1+b1
+
1
a2+b2
+…+
1
an+bn
＜
5
12
．
设函数f（x）=
1
x+1
，点A0表示坐标原点，点An（n，f（n））（n∈N*）．若向量an=
A0A1
+
A1A2
+…+
AN-1An
，θn是an与i的夹角（其中i=（1，0）），则tanθn=
 
．
已知Sn为等比数列{an}的前n项和，且a1+a4=-
7
16
，且对于任意的n∈N*，有Sn、Sn+2、Sn+1成等差数列，{bn}的前n项和Tn=
1
2
n2+
k
2
n（n∈N*，k＞0），且Tn的最小值为1．
（1）求数列{an}和{bn}的通项公式；
（2）对任意m∈N*，将数列{bn}中落入区间（2m+
9
2
，4m+
9
2
）内的个数记为cm，求数列{cm}的前m项和；
（3）记Pn=|
b1
a1
|+|
b2
a2
|+|
b3
a3
|+…+|
bn
an
|，若（n-1）2≤m（Pn-n-1）对于n≥2恒成立，求实数m的取值范围．
已知四面体O-ABC中，M、N分别是OA、BC的中点，P是MN上（靠近点M）的三等分点，其中OA=OB=OC=1，∠AOC=∠AOB=∠BOC=60°，求异面直线OP与AB所成角的余弦值．（用向量法）
定义域为R的函数f（x）满足f（x+2）=2f（x），当x∈[0，2）时，f（x）=
x2-x，x∈[0，1)
-(
1
2
)|x-
3
2
|，x∈[1，2)
则当x∈[-4，-2）时，函数f（x）的最小值为（　　）
A、-
1
16
B、-
1
4
C、-
1
2
D、-
1
8
已知函数f（x）=ex-（a+1）x（a∈R）
（1）当x＞0时，讨论函数f（x）的单调性；
（2）若x∈R，f（x）≥b（b∈R）恒成立，求（a+1）b的值域．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网