题目内容
讨论函数y=
在区间上的单调性．
| lnx |
| x |
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求出原函数的定义域，求出原函数的导函数，由导函数的零点对定义域分段，然后根据导函数在各区间段内的符号得到原函数的单调性．
解答：
证明：函数y=
的定义域为（0，+∞），
y′=
，由y′=0，得x=e．
当x∈（0，e）时，y′＞0，函数为增函数；
当x∈（e，+∞）时，y′＜0，函数为减函数．
| lnx |
| x |
y′=
| 1-lnx |
| x2 |
当x∈（0，e）时，y′＞0，函数为增函数；
当x∈（e，+∞）时，y′＜0，函数为减函数．
点评：本题考查了利用导数研究函数的单调性，主要考查导函数的正负与原函数的单调性之间的关系，即当导函数大于0时原函数单调递增，当导函数小于0时原函数单调递减，是基础题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
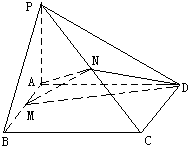已知：ABCD是矩形，设PA=a，PA⊥平面ABCD，M，N分别是AB，PC的中心点．
已知四面体O-ABC中，M、N分别是OA、BC的中点，P是MN上（靠近点M）的三等分点，其中OA=OB=OC=1，∠AOC=∠AOB=∠BOC=60°，求异面直线OP与AB所成角的余弦值．（用向量法）
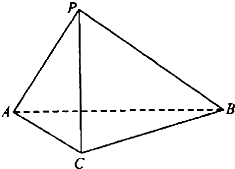如图，在三棱锥P-ABC中，AC=BC=2，∠ACB=90°，AP=BP=AB，PC⊥AC．