Question

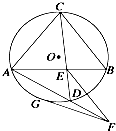
如图所示，圆O的两弦AB和CD交于点E，EF∥CB，EF交AD的延长线于点F，FG切圆O于点G．
（Ⅰ）求证：△DFE∽△EFA；
（Ⅱ）如果FG=1，求EF的长．

Answer 1

考点：相似三角形的判定,与圆有关的比例线段

专题：立体几何

分析：（Ⅰ）由同位角相等得出∠BCE=∠FED，由圆中同弧所对圆周角相等得出∠BAD=∠BCD，结合公共角∠EFD=∠EFD，证出△DEF∽△EFA；
（Ⅱ）由（Ⅰ）得EF²=FA•FD，再由圆的切线长定理FG²=FD•FA，所以FG=EF=1．

解答： 证明：（Ⅰ）∵EF∥CB，
∴∠DEF=∠DCB．
∴∠DEF=∠DAB，
∴∠DEF=∠DAB．
又∵∠DFE=∠EFA，
∴△DFE∽△EFA…（4分）
解：（Ⅱ）∵△DFE∽△EFA，
∴EF：FA=FD：EF．
∴EF²=FA•FD．
又∵FG切圆于G，
∴GF²=FA•FD．
∴EF²=FG²．
∴EF=FG．
已知EF=1，
∴FG=1…（8分）

点评：本题考查与圆有关的角、比例线段，要善于寻找有关线段的数量关系，结合相关性质、定理求解．