题目内容
12．已知函数f（x）=lnx+x，若函数f（x）在点P（x0，f（x0））处切线与直线3x-y+1=0平行，则x0=$\frac{1}{2}$．分析 求出导函数，利用切线斜率，然后即可．
解答 解：函数f（x）=lnx+x，
可得函数f′（x）=$\frac{1}{x}$+1，
函数f（x）在点P（x0，f（x0））处切线与直线3x-y+1=0平行，
可得：$\frac{1}{{x}_{0}}+1=3$，解得x0=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查函数的导数的应用，切线方程的求法，考查转化思想以及计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
3．下列结论不正确的是（ ）
| A． | 若y=3，则y'=0 | B． | 若$y=\frac{1}{{\sqrt{x}}}$，则$y'=-\frac{{\sqrt{x}}}{2}$ | C． | 若$y=\sqrt{x}$，则$y'=\frac{1}{{2\sqrt{x}}}$ | D． | 若y=x，则y'=1 |
20．已知tanα=-$\frac{3}{4}$，tan（π-β）=$\frac{1}{2}$，则tan（α-β）的值为（ ）
| A． | -$\frac{2}{11}$ | B． | $\frac{2}{11}$ | C． | $\frac{11}{2}$ | D． | -$\frac{11}{2}$ |
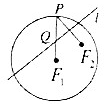如图，已知圆F1的半径为4，|F1F2|=2，P是圆F1上的一个动点，F2P的中垂线l交F1P于点Q，以直线F1F2为x轴，F1F2的中垂线为y轴建立平面直角坐标系．
2．$\sqrt{1-{{sin}^2}\frac{π}{5}}$的化简结果是（ ）
| A． | $cos\frac{π}{5}$ | B． | $-cos\frac{π}{5}$ | C． | $±cos\frac{π}{5}$ | D． | $sin\frac{π}{5}$ |