题目内容
4.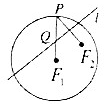 如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.
如图,已知圆F1的半径为4,|F1F2|=2,P是圆F1上的一个动点,F2P的中垂线l交F1P于点Q,以直线F1F2为x轴,F1F2的中垂线为y轴建立平面直角坐标系.(1)求点Q的轨迹E的方程;
(2)设过点F2的动直线m与轨迹E交于A,B两点,在x轴上是否存在定点R,使得$\overrightarrow{RA}$$•\overrightarrow{RB}$是定值?若存在,求出点R的坐标和定值;若不存在,请说明埋由.
分析 (1)由题意可知:丨QF2丨+丨QF1丨=4>|F1F2|=2,Q的轨迹E为以F1,F2为焦点,4为长轴长的椭圆,由椭圆的性质即可求得椭圆的标准方程;
(2)设直线m的方程x=my+1,代入椭圆方程,由韦达定理及向量数量积的坐标运算,求得$\overrightarrow{RA}$$•\overrightarrow{RB}$=$\frac{3{m}^{2}({t}^{2}-4)+4{t}^{2}-8t-5}{3{m}^{2}+4}$,使得$\overrightarrow{RA}$$•\overrightarrow{RB}$是定值,则$\left\{\begin{array}{l}{{t}^{2}-4=λ}\\{4{t}^{2}-8t-5=4λ}\end{array}\right.$,即可求得m和λ的值.
解答  解:(1)由题意可知:丨PQ丨+丨QF1丨=丨PF1丨=r=4,
解:(1)由题意可知:丨PQ丨+丨QF1丨=丨PF1丨=r=4,
由F2P的中垂线l交F1P于点Q,则丨QF2丨=丨PQ丨,
∴丨QF2丨+丨QF1丨=4>|F1F2|=2,
则点Q的轨迹E为以F1,F2为焦点,4为长轴长的椭圆,
即2a=4,2c=2,b2=a2-c2=3,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设x轴上存在一点R(t,0),使得 $\overrightarrow{RA}$•$\overrightarrow{RB}$为定值数
①直线l的斜率存在,设直线m的方程为x=my+1,A(x1,y1 ),B(x2,y2),
把直线l的方程代入椭圆方程化简可得(3m2+4)y2+6my-9=0,
显然△=36m2+36(3m2+4)=144(m2+1)>0
∴y1+y2=-$\frac{6m}{3{m}^{2}+4}$,y1y2=-$\frac{9}{3{m}^{2}+4}$,
$\overrightarrow{RA}$•$\overrightarrow{RB}$=(x1-t,y1 )(x2-t,y2)=x1x2-t(x1+x2)+t2+y1y2,
=(1+m2)y1y2+m(1-t)(y1+y2)+t2-2t+1,
=$\frac{3{m}^{2}({t}^{2}-4)+4{t}^{2}-8t-5}{3{m}^{2}+4}$,
若存在R(t,0),使$\frac{3{m}^{2}({t}^{2}-4)+4{t}^{2}-8t-5}{3{m}^{2}+4}$=λ成立,
则$\left\{\begin{array}{l}{{t}^{2}-4=λ}\\{4{t}^{2}-8t-5=4λ}\end{array}\right.$,解得:$\left\{\begin{array}{l}{t=\frac{11}{8}}\\{λ=-\frac{135}{64}}\end{array}\right.$,
故存在R($\frac{11}{8}$,0),使得使得$\overrightarrow{RA}$$•\overrightarrow{RB}$是定值-$\frac{135}{64}$.
点评 本题考查椭圆的定义,直线与椭圆的位置关系,考查韦达定理及向量数量积的坐标运算,考查计算能力,属于中档题.

| A. | 在平面α内存在直线a与直线l平行 | B. | 在平面α内存在直线a与直线l垂直 | ||
| C. | 在平面α内存在直线a与直线l相交 | D. | 在平面α内存在直线a与直线l异面 |
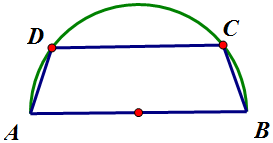 有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.
有一块半径为2的半圆形钢板,计划裁剪成等腰梯形ABCD的形状,它的下底AB是半圆的直径,上底CD的端点在半圆上.