题目内容
20．已知tanα=-$\frac{3}{4}$，tan（π-β）=$\frac{1}{2}$，则tan（α-β）的值为（ ）| A． | -$\frac{2}{11}$ | B． | $\frac{2}{11}$ | C． | $\frac{11}{2}$ | D． | -$\frac{11}{2}$ |
分析 由已知利用诱导公式可求tanβ，进而利用两角差的正切函数公式即可计算得解．
解答 解：∵tanα=-$\frac{3}{4}$，tan（π-β）=-tanβ=$\frac{1}{2}$，可得：tanβ=-$\frac{1}{2}$，
∴tan（α-β）=$\frac{tanα-tanβ}{1+tanαtanβ}$=$\frac{（-\frac{3}{4}）-（-\frac{1}{2}）}{1+（-\frac{3}{4}）×（-\frac{1}{2}）}$=-$\frac{2}{11}$．
故选：A．
点评 本题主要考查了诱导公式，两角差的正切函数公式在三角函数化简求值中的应用，考查了计算能力和转化思想，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
5．下列说法中正确的是（ ）
| A． | 命题“?x∈R．ex＞0”的否定是“?x∈R，ex＞0” | |
| B． | 命题“若a=-1，则函数f（x）=ax2+2x-1只有一个零点”的逆命题是真命题 | |
| C． | “x2+2x≥ax在x∈[1，2]上恒成立”?“对于x∈[1，2]有（x2+2x）min≥（ax）max” | |
| D． | 命题“已知x，y∈R，若x+y≠3，则x≠2或y≠1”是真命题 |
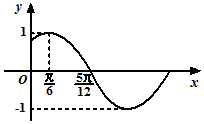已知函数$f（x）=Msin（ωx+φ）（M＞0，|φ|＜\frac{π}{2}）$的部分图象如图所示．