题目内容
1.命题p:“关于x的不等式x2+(a-1)x+a2≤0,(a>0)的解集为∅”,命题q:“在区间[-2,4]上随机地取一个数x,若x满足|x|≤a(a>0)的概率$P≥\frac{5}{6}$”,当“p∧q”与“p∨q”一真一假时,求实数a的取值范围.分析 当“p∧q”与“p∨q”一真一假时,则p与q一真一假时,进而可得实数a的取值范围.
解答 解:命题p:因为关于x的不等式x2+(a-1)x+a2≤0的解集为∅
所以:x2+(a-1)x+a2=0对应的△<0即:3a2+2a-1>0,
即:a<-1或$a>\frac{1}{3}$,又a>0,所以:$a>\frac{1}{3}$
命题q:“在区间[-2,4]上随机地取一个数x,若x满足|x|≤a(a>0)的概率$P≥\frac{5}{6}$”
因为|x|≤a(a>0),所以-a<x<a
当a≤2时,则$P≤\frac{2}{3}$不满足条件,
当a>2时,则$P=\frac{a-(-2)}{6}≥\frac{5}{6}$,所以a≥3
当“p∧q”与“p∨q”一真一假时,则p与q一真一假时,
当p真q假时,a∈$(\frac{1}{3},3)$,
当p假q值时,不存在满足条件的a值,
综上可得到实数a的取值范围:$(\frac{1}{3},3)$.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,二次不等式的解法,几何概型难度中档.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
9.函数f(x)=x2-2ax-2alnx(a∈R),则下列说法不正确的命题个数是( )
①当a<0时,函数y=f(x)有零点;
②若函数y=f(x)有零点,则a<0;
③存在a>0,函数y=f(x)有唯一的零点;
④若a≤1,则函数y=f(x)有唯一的零点.
①当a<0时,函数y=f(x)有零点;
②若函数y=f(x)有零点,则a<0;
③存在a>0,函数y=f(x)有唯一的零点;
④若a≤1,则函数y=f(x)有唯一的零点.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.若角θ是第四象限的角,则角${-^{\;}}\frac{θ}{2}$是( )
| A. | 第一、三象限角 | B. | 第二、四象限角 | C. | 第二、三象限角 | D. | 第一、四象限角 |
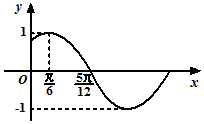 已知函数$f(x)=Msin(ωx+φ)(M>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Msin(ωx+φ)(M>0,|φ|<\frac{π}{2})$的部分图象如图所示.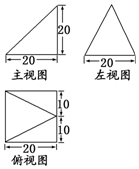 已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.
已知某个几何体的三视图如图,根据图中标出的尺寸(单位:cm),可得这个几何体的体积是$\frac{8000}{3}$ cm3.