题目内容
已知f(x)=-2|2|x|-1|+1和g(x)=x2-2|x|+m(m∈R)是定义在R上的两个函数,则下列命题:
①函数f(x)的图象关于直线x=0对称;
②关于x的方程f(x)-k=0恰有四个不相等实数根的充要条件是k∈(0,1);
③关于x的方程f(x)=g(x)恰有四个不相等实数根的充要条件是m∈[0,1];
④若?x1∈[-1,1],?x2∈[-1,1],f(x1)<g(x2)成立,则m∈(-1,+∞);
其中正确的例题有 (写出所有正确例题的序号).
①函数f(x)的图象关于直线x=0对称;
②关于x的方程f(x)-k=0恰有四个不相等实数根的充要条件是k∈(0,1);
③关于x的方程f(x)=g(x)恰有四个不相等实数根的充要条件是m∈[0,1];
④若?x1∈[-1,1],?x2∈[-1,1],f(x1)<g(x2)成立,则m∈(-1,+∞);
其中正确的例题有
考点:命题的真假判断与应用
专题:简易逻辑
分析:画出函数f(x)=-2|2|x|-1|+1的图象,利用图象法可判断①和②,分析指定区间上f(x)与g(x)的值域,进而将存在性问题转化为最值问题后,可判断③和④
解答:
解:因为f(x)=-2|2|x|-1|+1为偶函数,所以函数f(x)的图象关于直线x=0对称,故①正确;
作出f(x)=-2|2|x|-1|+1如图所示,可知,关于x的方程f(x)-k=0恰有四个不相等实数根的充要条件为k∈(-1,1),故②错误;
在同一坐标系中作出f(x)=-2|2|x|-1|+1和y=x2-2|x|的图象,由图象可知当m∈(-1,
)时方程f(x)=g(x)恰有四个不相等实数根,故③错;
由题可知,只需当x∈[-1,1]时f(x)min<g(x)max即可.易得f(x)min=-1,g(x)max=m,所以m∈(-1,+∞),所以④正确.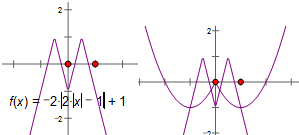
故答案为:①④.
作出f(x)=-2|2|x|-1|+1如图所示,可知,关于x的方程f(x)-k=0恰有四个不相等实数根的充要条件为k∈(-1,1),故②错误;
在同一坐标系中作出f(x)=-2|2|x|-1|+1和y=x2-2|x|的图象,由图象可知当m∈(-1,
| 7 |
| 4 |
由题可知,只需当x∈[-1,1]时f(x)min<g(x)max即可.易得f(x)min=-1,g(x)max=m,所以m∈(-1,+∞),所以④正确.

故答案为:①④.
点评:本题考查命题的真假的判断与应用,充要条件的判断,函数的最值以及函数的图象的应用,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知y=x-
(k≠0),若f′(1)=
则k等于( )
| k |
| x |
| 1 |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若方程lnx+x-5=0在区间(a,b)(a,b∈Z,且b-a=1)上有一实根,则a的值为( )
| A、5 | B、4 | C、3 | D、2 |
 从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.
从某企业生产的某种产品中抽取500件,测量这些产品的一项质量指标值,由测量结果得到如图所示的频率分布直方图.