题目内容
年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人,他们的健康状况如下表:
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”.
(Ⅰ)随机访问该小区一位80岁以下的老龄人,该老龄人生活能够自理的概率是多少?
(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
| 健康指数 | 2 | 1 | 0 | -1 |
| 60岁至79岁的人数 | 120 | 133 | 32 | 15 |
| 80岁及以上的人数 | 9 | 18 | 14 | 9 |
(Ⅰ)随机访问该小区一位80岁以下的老龄人,该老龄人生活能够自理的概率是多少?
(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.求被访问的3位老龄人中恰有1位老龄人的健康指数不大于0的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)求出该小区80岁以下的老龄人数,即可求解老龄人生活能够自理的概率.
(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.写出5人中抽取3人的基本事件总数,被访问的3位老龄人中恰有1位老龄人的个数,即可求解健康指数不大于0的概率.
(Ⅱ)按健康指数大于0和不大于0进行分层抽样,从该小区的老龄人中抽取5位,并随机地访问其中的3位.写出5人中抽取3人的基本事件总数,被访问的3位老龄人中恰有1位老龄人的个数,即可求解健康指数不大于0的概率.
解答:
解:(Ⅰ)解:该社区80岁以下的老龄人共有120+133+32+15=300人,…(1分)
其中生活能够自理的人有120+133+32=285人,…(2分)
记“随机访问该小区一位80岁以下的老龄人,该老人生活能够自理”为事件A,
则P(A)=
=
. …(4分)
(Ⅱ)根据表中数据可知,社区健康指数大于0的老龄人共有280人,
不大于0的老龄人共有70人,…(5分)
所以,按照分层抽样,被抽取的5位老龄人中,有
×5=4位为健康指数大于0的,
依次记为:a,b,c,d,有一位健康指数不大于0的,记为e. …(7分)
从这5人中抽取3人的基本事件有:(a,b,c)(a,b,d)(a,b,e)(a,c,d)(a,c,e)(a,d,e)
(b,c,d)(b,c,e)(b,d,e)(c,d,e)共10种,…(9分)
其中恰有1位老龄人的健康指数不大于0的事件有:(a,b,e) (a,c,e)
(a,d,e) (b,c,e)(b,d,e)(c,d,e)共6种,…(10分)
记“被访问的3位老龄人中恰有1位老龄人的健康指数不大于0”为事件B,
则P(B)=
=
…(12分)
其中生活能够自理的人有120+133+32=285人,…(2分)
记“随机访问该小区一位80岁以下的老龄人,该老人生活能够自理”为事件A,
则P(A)=
| 285 |
| 300 |
| 19 |
| 20 |
(Ⅱ)根据表中数据可知,社区健康指数大于0的老龄人共有280人,
不大于0的老龄人共有70人,…(5分)
所以,按照分层抽样,被抽取的5位老龄人中,有
| 280 |
| 350 |
依次记为:a,b,c,d,有一位健康指数不大于0的,记为e. …(7分)
从这5人中抽取3人的基本事件有:(a,b,c)(a,b,d)(a,b,e)(a,c,d)(a,c,e)(a,d,e)
(b,c,d)(b,c,e)(b,d,e)(c,d,e)共10种,…(9分)
其中恰有1位老龄人的健康指数不大于0的事件有:(a,b,e) (a,c,e)
(a,d,e) (b,c,e)(b,d,e)(c,d,e)共6种,…(10分)
记“被访问的3位老龄人中恰有1位老龄人的健康指数不大于0”为事件B,
则P(B)=
| 6 |
| 10 |
| 3 |
| 5 |
点评:本题考查分层抽样,古典概型概率公式的应用,基本知识的考查.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
若log23=
,则3x=( )
| 1 |
| x |
| A、1 | B、3 |
| C、log23 | D、2 |
直线ax+by+b-a=0与圆(x+2)2+(y-3)2=25 位置关系为( )
| A、相交或相切 | B、相切 |
| C、相离 | D、不确定 |
如果在△ABC中,a=3,b=
,c=2,那么B等于( )
| 7 |
A、
| ||
B、
| ||
C、
| ||
D、
|
两条直线y=ax-2和y=(a+2)x+1互相垂直的充要条件是( )
| A、a=2 | B、a=1 |
| C、a=0 | D、a=-1 |
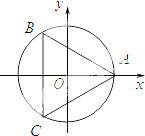 如图,在单位圆中,用三角形的重心公式
如图,在单位圆中,用三角形的重心公式