题目内容
10．设x1，x2，x3，x4，x5是1，2，3，4，5的任一排列，则x1+2x2+3x3+4x4+5x5的最小值是35．分析 利用反序排列，推出结果即可．
解答 解：由题意可知：x1，x2，x3，x4，x5是1，2，3，4，5的反序排列时，x1+2x2+3x3+4x4+5x5取得最小值：
解：1×5+2×4+3×3+4×2+5×1=35．
故答案为：35．
点评 本题考查反序排列的性质，考查计算能力．
练习册系列答案
口算能手系列答案
相关题目
2．
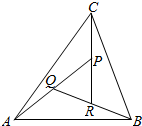如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点为P，若$\overrightarrow{AP}=m\vec a+n\vec b$，则m、n对应的值为 （ ）
如图，在△ABC中，设$\overrightarrow{AB}=\overrightarrow a$，$\overrightarrow{AC}=\overrightarrow b$，AP的中点为Q，BQ的中点为R，CR的中点为P，若$\overrightarrow{AP}=m\vec a+n\vec b$，则m、n对应的值为 （ ）| A． | $\frac{2}{7}，\frac{4}{7}$ | B． | $\frac{1}{2}，\frac{1}{4}$ | C． | $\frac{1}{6}，\frac{2}{7}$ | D． | $\frac{1}{6}，\frac{3}{7}$ |
19．已知O为坐标原点，A，B两点的坐标均满足不等式组$\left\{\begin{array}{l}{x-3y+1≤0}\\{x+y-3≤0}\\{x-1≥0}\end{array}\right.$，设$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为θ，则sinθ的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{4\sqrt{65}}{65}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{5}$ |