题目内容
如图所示，把等腰直角三角形ABC沿斜边AB旋转至△ABD的位置，使CD=AC，求证：平面ABD⊥平面ABC．考点：平面与平面垂直的判定
专题：空间位置关系与距离
分析：取AB中点E，连接DE，DE⊥AB，连接CE，CE⊥AB，从而DE⊥CE，由此能证明平面ABD⊥平面ABC．
解答：
证明：取AB中点E，连接DE，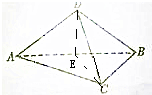
∵△ABD是等腰直角三角形，
∴DE⊥AB，且DE=
，
连接CE，同理CE⊥AB，且CE=
，
∵AD=AC，∴CE=DE=
，
∵CD=AC，∴CE2+DE2=CD2，
∴△CDE为等腰直角三角形，DE⊥CE，
∵AB∩CE于E，∴DE⊥平面ABC，
又∵DE?平面ABD，
∴平面ABD⊥平面ABC．
∵△ABD是等腰直角三角形，
∴DE⊥AB，且DE=
| AD | ||
|
连接CE，同理CE⊥AB，且CE=
| AC | ||
|
∵AD=AC，∴CE=DE=
| AC | ||
|
∵CD=AC，∴CE2+DE2=CD2，
∴△CDE为等腰直角三角形，DE⊥CE，
∵AB∩CE于E，∴DE⊥平面ABC，
又∵DE?平面ABD，
∴平面ABD⊥平面ABC．
点评：本题考查平面与平面垂直的证明，是中档题，解题时要注意空间思维能力的培养．
练习册系列答案
相关题目
给出下列四个命题，其中不正确的是（ ）
| A、函数y=tanx是增函数 | ||
B、y=|sin2x|的最小正周期是
| ||
C、函数y=cosx在[2kπ+π，2kπ+
| ||
D、函数y=tan（x+
|
如图所示，已知抛物线y=x2的动弦AB所在直线与圆x2+y2=1相切，分别过点A、B的抛物线的两条切线相交于点M，求点M的轨迹方程．