题目内容
线段AB长为2a，两端点A，B分别在一个直二面角的两个面内，且AB与两个面所成的角分别为30°和45°，设A，B两点在二面角棱上的射影分别为A′，B′，则A′B′的长为（ ）
A、
| ||||
B、
| ||||
| C、a | ||||
| D、2a |
考点：点、线、面间的距离计算
专题：空间位置关系与距离
分析：利用直线与平面所成角的定义和垂直关系，得：∠BAB′=30°，∠ABA′=45°，由此能求出A′B′的长．
解答：
解：利用直线与平面所成角的定义和垂直关系，
得：∠BAB′=30°，∠ABA′=45°，
∴在Rt△BB′A中，BB′=
=a，
在Rt△BA′A中，BA′=
AB=
a，
∴在Rt△BB′A′中，
A′B′=
=
=a．
故选：C．
得：∠BAB′=30°，∠ABA′=45°，
∴在Rt△BB′A中，BB′=
| AB |
| 2 |
在Rt△BA′A中，BA′=
| ||
| 2 |
| 2 |
∴在Rt△BB′A′中，
A′B′=
| BA′2-BB′2 |
| 2a2-a2 |
故选：C．
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，把等腰直角三角形ABC沿斜边AB旋转至△ABD的位置，使CD=AC，求证：平面ABD⊥平面ABC．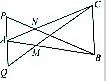
在△ABC中，在AC上取点N，使AC=3AN，在AB上取点M，使AB=3AM，在BN的延长线上取点P，使BN=2NP，在CM的延长线上取点Q，使CM=2MQ，如图所示，记向量