题目内容
已知函数f(x)=lnx,g(x)=
x2-bx(b为常数),若b>1对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,则实数b的取值范围是 .
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:
分析:要使得对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,利用导数的几何意义是切线的斜率,得到对于区间[1,2]上的任意实数x,|f′(x)|>|g′(x)|,列出b的不等关系,从而得出b的取值范围.
解答:
解:对于区间[1,2]上的任意实数x,f′(x)=
∈[
,1].
g′(x)=x-b∈[1-b,2-b],
要使得对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,
若用注意到f(x)是增函数,不妨设x1>x2,则f(x1)>f(x2),问题转化为|f(x1)-f(x2)|>|g(x1)-g(x2)|
等价于-f(x1)+f(x2)<g(x1)-g(x2)<f(x1)-f(x2)从而f(x1)-g(x1)>f(x2)-g(x2)且f(x1)+g(x1)>f(x2)+g(x2),
即f(x)-g(x)与f(x)+g(x)都是增函数,
利用导数的几何意义是切线的斜率,得到|f′(x)|>|g′(x)|,
即
>|b-x|,于是x-
≤b≤x+
即(x-
)max≤b≤(x+
)min
∴
≤b≤2.
则b的取值范围[
,2].
故答案为:[
,2].
| 1 |
| x |
| 1 |
| 2 |
g′(x)=x-b∈[1-b,2-b],
要使得对于区间[1,2]上的任意两个不相等的实数x1,x2,都有|f(x1)-f(x2)|>|g(x1)-g(x2)|成立,
若用注意到f(x)是增函数,不妨设x1>x2,则f(x1)>f(x2),问题转化为|f(x1)-f(x2)|>|g(x1)-g(x2)|
等价于-f(x1)+f(x2)<g(x1)-g(x2)<f(x1)-f(x2)从而f(x1)-g(x1)>f(x2)-g(x2)且f(x1)+g(x1)>f(x2)+g(x2),
即f(x)-g(x)与f(x)+g(x)都是增函数,
利用导数的几何意义是切线的斜率,得到|f′(x)|>|g′(x)|,
即
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
∴
| 3 |
| 2 |
则b的取值范围[
| 3 |
| 2 |
故答案为:[
| 3 |
| 2 |
点评:本题考查导数在最大值、最小值问题中的应用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
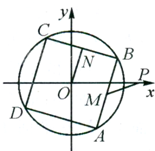 如图,已知点P(
如图,已知点P(| 2 |
| PM |
| ON |
| A、[-2,2] | ||||||||
B、[-
| ||||||||
| C、[-1,1] | ||||||||
D、[-
|
已知等差数列{an}中,前19项和为95,则a10等于( )
| A、19 | B、10 | C、9 | D、5 |
在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且
=α
+β
,则( )
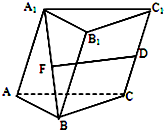
| DF |
| AB |
| AC |

A、α=
| ||
B、α=-
| ||
C、α=1,β=-
| ||
D、α=-1,β=
|