题目内容
在三棱柱ABC-A1B1C1中,D是CC1的中点,F是A1B的中点,且
=α
+β
,则( )
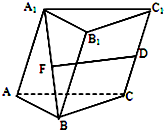
| DF |
| AB |
| AC |

A、α=
| ||
B、α=-
| ||
C、α=1,β=-
| ||
D、α=-1,β=
|
考点:向量在几何中的应用
专题:空间向量及应用
分析:根据向量加法的多边形法则可得,
=
+
+
=
+
+
=
+
-
+
+
=
-
,从而可求α,β.
| DF |
| DC |
| CB |
| BF |
| 1 |
| 2 |
| C1C |
| CB |
| 1 |
| 2 |
| BA1 |
| 1 |
| 2 |
| A1A |
| AB |
| AC |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| AA1 |
| 1 |
| 2 |
| AB |
| AC |
解答:
解:根据向量加法的多边形法则以及已知可得,
=
+
+
=
+
+
=
+
-
+
+
=
-
,
∴α=
,β=-1,
故选A.
| DF |
| DC |
| CB |
| BF |
| 1 |
| 2 |
| C1C |
| CB |
| 1 |
| 2 |
| BA1 |
| 1 |
| 2 |
| A1A |
| AB |
| AC |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| AA1 |
| 1 |
| 2 |
| AB |
| AC |
∴α=
| 1 |
| 2 |
故选A.
点评:本题主要考查了平面向量加法的三角形法则及多边形法则的应用,解题的关键是要善于利用题目中正三棱柱的性质,把所求的向量用基本向量表示.

练习册系列答案
相关题目
如果不等式|x-a|<1成立的充分不必要条件是1<x<2,则实数a的取值范围是( )
| A、1<a<2 |
| B、1≤a≤2 |
| C、a>2或a<1 |
| D、a≥2或a≤1 |
已知向量|
|=2,|
|=1,且
,
夹角为60°,则向量
+
与
-
的夹角的余弦的值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、3 | ||||
B、
| ||||
C、
| ||||
D、
|
二次函数y=x2(x>0)的图象在点(an,an2)处的切线与x轴交点的横坐标为an+1,n为正整数,a1=
,则S5=( )
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
数列{an}满足a1=1,an+4an-1=0(n≥2),则a2与a4的等比中项是( )
| A、4 | B、±4 | C、16 | D、±16 |
从2010名学生中选50人组成参观团,先用简单随机抽样方法剔除10人,再将其余2000人按系统抽样方法选取,则每人入选的概率( )
| A、不全相等 | ||
| B、B均不相等 | ||
C、都是
| ||
D、都是
|
复数z=i2(1-i)(其中i为虚数单位)的值是( )
| A、1-i | B、1+i |
| C、-1-i | D、-1+i |
设全集U=R,A={x|x(x-2)<0},B={x|y=ln(1-x)<0},则图中阴影部分表示的集合为( )
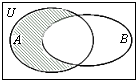

| A、{x|0<x≤1} |
| B、{x|1≤x<2} |
| C、{x|x≥1} |
| D、{x|x≤1} |