题目内容
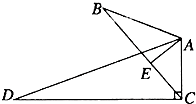
如图，∠B=∠D，AE⊥BC，∠ACD=90°且AB=6，AC=4，AD=12，则AE= ．
考点：余弦定理,正弦定理
专题：解三角形
分析：先在△ACD中，由AC与AD利用勾股定理求出DC的长，继而求出cosD，得到cosB的值，在△ABE中，利用锐角三角函数定义表示出cosB，将cosB与AB的长代入求出BE的长，再利用勾股定理即可求出AE的长．
解答：
解：在△ACD中，AC=4，AD=12，∠ACD=90°，
∴根据勾股定理得：DC=
=8
，
∴cosD=
=
，
∵∠B=∠D，AE⊥BC，AB=6，
∴cosB=
，即
=
，
解得：BE=4
，
根据勾股定理得：AE=
=2．
故答案为：2
∴根据勾股定理得：DC=
| AD2-AC2 |
| 2 |
∴cosD=
8
| ||
| 12 |
2
| ||
| 3 |
∵∠B=∠D，AE⊥BC，AB=6，
∴cosB=
| BE |
| AB |
2
| ||
| 3 |
| BE |
| 6 |
解得：BE=4
| 2 |
根据勾股定理得：AE=
| AB2-BE2 |
故答案为：2
点评：此题考查了正弦定理，锐角三角函数定义，以及勾股定理，熟练掌握正弦定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某企业2月份的产量与1月份相比增长率为p，3月份的产量与2月份相比增长率为q（p＞0，q＞0），若该企业这两个月产量的平均增长率为x，则下列关系中正确的是（ ）
A、x≥
| ||
B、x≤
| ||
C、x＞
| ||
D、x＜
|
二次函数y=x2（x＞0）的图象在点（an，an2）处的切线与x轴交点的横坐标为an+1，n为正整数，a1=
，则S5=（ ）
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|