题目内容

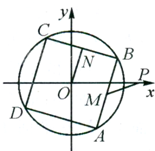如图，已知点P(
2
，0)，正方形ABCD内接于圆O：x2+y2=1，M、N分别为边AB、BC的中点．当正方形ABCD绕圆心O旋转时，
PM
•
ON
的取值范围为（　　）
A、[-2，2]
B、[-
2
，
2
]
C、[-1，1]
D、[-
2
2
，
2
2
]
考点：平面向量数量积的运算,平面向量的坐标运算
专题：平面向量及应用
分析：由已知，将
PM
•
ON
转化为
PM
•
ON
=(
OM
-
OP
)•
ON
=
OM
•
ON
-
OP
•
ON
，得到
PM
•
ON
=-cos∠PON，结合角的范围求余弦值是范围．
解答： 解：
PM
•
ON
=(
OM
-
OP
)•
ON
=
OM
•
ON
-
OP
•
ON
=0-
2
×
2
2
cos∠PON=-cos∠PON
∵∠PON∈R，∴cos∠PON∈[-1，1]，
∴
PM
•
ON
的取值范围为[-1，1]．
故选C．
点评：本题考查了向量的加减运算以及向量数量积的运算，本题注意利用余弦值的范围求向量的数量积的范围．
练习册系列答案
相关题目
不等式
x+2
1-2x
≥0的解集是
 
．
直线l1：ax-y+2a+1=0和l2：2x-（a-1）y+2=0，若l1⊥l2，则a=
 
．
已知函数f（x）=lnx，g（x）=
1
2
x2-bx（b为常数），若b＞1对于区间[1，2]上的任意两个不相等的实数x1，x2，都有|f（x1）-f（x2）|＞|g（x1）-g（x2）|成立，则实数b的取值范围是
 
．
对于平面几何中的命题“如果两个角的两边分别对应垂直，那么这两个角相等或互补”，在立体几何中，类比上述命题，可以得到命题：“
 
”．
用数学归纳法证明：1+
1
22
+
1
32
+…+
1
(2n)2
＜2-
1
2n
（n∈N*），第二步证明“从k到k+1”，左端增加的项数是（　　）
A、1B、2C、2kD、8k+4
某企业2月份的产量与1月份相比增长率为p，3月份的产量与2月份相比增长率为q（p＞0，q＞0），若该企业这两个月产量的平均增长率为x，则下列关系中正确的是（　　）
A、x≥
p+q
2
B、x≤
p+q
2
C、x＞
p+q
2
D、x＜
p+q
2
如果不等式|x-a|＜1成立的充分不必要条件是1＜x＜2，则实数a的取值范围是（　　）
A、1＜a＜2
B、1≤a≤2
C、a＞2或a＜1
D、a≥2或a≤1
从2010名学生中选50人组成参观团，先用简单随机抽样方法剔除10人，再将其余2000人按系统抽样方法选取，则每人入选的概率（　　）
A、不全相等
B、B均不相等
C、都是
5
201
D、都是
1
40

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网