题目内容
3．若函数f（x）=alog2（|x|+4）+x2+a2-8有唯一的零点，则实数a的值是（ ）| A． | -4 | B． | 2 | C． | ±2 | D． | -4或2 |
分析 根据f（x）是偶函数可知唯一零点比为0，从而得出a，再利用函数图象验证即可．
解答 解：显然f（x）是偶函数，
∵f（x）有唯一一个零点，∴f（0）=0，即a2+2a-8=0，
解得a=2或a=-4．
当a=2时，f（x）=2alog2（|x|+4）+x2-4，
∴f（x）在[0，+∞）上单调递增，符合题意；
当a=-4时，f（x）=-4log2（|x|+4）+x2+8，
作出y=4log2（|x|+4）和y=x2+8的函数图象如图所示：
由图象可知f（x）有三个零点，不符合题意；
综上，a=2．
故选B．
点评 本题考查了函数零点与函数图象的关系，属于中档题．
练习册系列答案
相关题目
14．若圆x2+y2-12x+16=0与直线y=kx交于不同的两点，则实数k的取值范围为（ ）
| A． | （-$\sqrt{3}$，$\sqrt{3}$） | B． | （-$\sqrt{5}$，$\sqrt{5}$） | C． | （-$\frac{\sqrt{5}}{2}$，$\frac{\sqrt{5}}{2}$） | D． | （-$\frac{\sqrt{3}}{2}$，$\frac{\sqrt{3}}{2}$） |
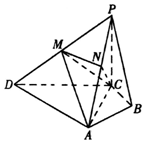在四棱锥P-ABCD中，PC⊥底面ABCD，M，N分别是PD，PA的中点，AC⊥AD，∠ACD=∠ACB=60°，PC=AC．
如图，已知函数y=2kx（k＞0）与函数y=x2的图象所围成的阴影部分的面积为$\frac{32}{3}$，则实数k的值为2．
如图，在四棱锥P-ABCD中，底面ABCD为梯形，CD∥AB，AB=2CD，AC交BD于O，锐角△PAD所在平面⊥底面ABCD，PA⊥BD，点Q在侧棱PC上，且PQ=2QC．