题目内容
13. 如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.
如图,在四棱锥P-ABCD中,底面ABCD为梯形,CD∥AB,AB=2CD,AC交BD于O,锐角△PAD所在平面⊥底面ABCD,PA⊥BD,点Q在侧棱PC上,且PQ=2QC.求证:(1)PA∥平面QBD;
(2)BD⊥AD.
分析 (1)连接OQ,可得PA∥OQ,即可证得PA∥平面QBD.
(2)在平面PAD内过P作PH⊥AD于H,可得PH⊥平面ABCD,即可得PH⊥BD,可得到以BD⊥平面PAD,即BD⊥AD.
解答 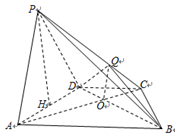 解:(1)如图,连接OQ,因为AB∥CD,AB=2 CD,
解:(1)如图,连接OQ,因为AB∥CD,AB=2 CD,
所以AO=2OC,又PQ=2QC,
所以PA∥OQ,…(3分)
又OQ?平面QBD,PA?平面QBD,
所以PA∥平面QBD.…(6分)
(2)在平面PAD内过P作PH⊥AD于H,因为侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD,
PH?平面PAD,所以PH⊥平面ABCD,…(9分)
又BD?平面ABCD,所以PH⊥BD,又PA⊥BD,
且PA和PH是平面PAD内的两条相交直线,所以BD⊥平面PAD,…(12分)
又AD?平面PAD,所以BD⊥AD.…(14分)
点评 本题考查了空间线面平行的判定,线线垂直的判定,考查了转化思想,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
3.若函数f(x)=alog2(|x|+4)+x2+a2-8有唯一的零点,则实数a的值是( )
| A. | -4 | B. | 2 | C. | ±2 | D. | -4或2 |
18.a2+b2=1是asinθ+bcosθ≤1恒成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.某投资公司现提供两种一年期投资理财方案,一年后投资盈亏的情况如表:
( I)甲、乙两人在投资顾问的建议下分别选择“投资股市”和“购买基金”,若一年后他们中至少有一人盈利的概率大于$\frac{4}{5}$,求p的取值范围;
( II)某人现有10万元资金,决定在“投资股市”和“购买基金”这两种方案中选出一种,若购买基金现阶段分析出$p=\frac{1}{2}$,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
| 投资股市 | 获利40% | 不赔不赚 | 亏损20% | 购买基金 | 获利20% | 不赔不赚 | 亏损10% |
| 概率P | $\frac{1}{2}$ | $\frac{1}{8}$ | $\frac{3}{8}$ | 概率P | p | $\frac{1}{3}$ | q |
( II)某人现有10万元资金,决定在“投资股市”和“购买基金”这两种方案中选出一种,若购买基金现阶段分析出$p=\frac{1}{2}$,那么选择何种方案可使得一年后的投资收益的数学期望值较大?
12.圆ρ=4cosθ的圆心到直线tanθ=1的距离为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
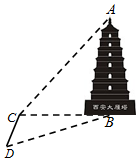 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面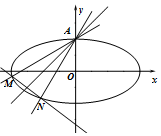 如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.
如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.