题目内容
11.已知数列{an}的前n项和Sn满足Sn=2an-a1,且a1,a2+1,a3成等差数列.(1)求数列{an}的通项公式;
(2)设bn=$\frac{2^n}{{{S_n}{S_{n+1}}}}$,求数列{bn}的前n项和Tn.
分析 (1)由Sn=2an-a1,利用an=Sn-Sn-1(n≥2),可得an=2an-1(n≥2),数列{an}是以2为公比的等比数列,又a1,a2+1,a3成等差数列,可得a1+a3=2(a2+1),解得a1,即可得出.
(2)由(1)得${S_n}={2^{n+1}}-2$,可得bn=$\frac{2^n}{{{S_n}{S_{n+1}}}}$=$\frac{1}{4}$$(\frac{1}{{2}^{n}-1}-\frac{1}{{2}^{n+1}-1})$,利用裂项求和方法即可得出.
解答 解:(1)因为Sn=2an-a1,所以an=Sn-Sn-1(n≥2),
即an=2an-1(n≥2),即数列{an}是以2为公比的等比数列,
又a1,a2+1,a3成等差数列,所以a1+a3=2(a2+1),即a1+4a1=2(2a1+1),解得a1=2,
所以数列{an}的通项公式为${a_n}={2^n}$.
(2)由(1)得${S_n}={2^{n+1}}-2$,所以${b_n}=\frac{2^n}{{{S_n}{S_{n+1}}}}=\frac{2^n}{{({2^{n+1}}-2)({2^{n+2}}-2)}}=\frac{2^n}{{4({2^n}-1)({2^{n+1}}-1)}}$=$\frac{1}{4}(\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}})$,
${T_n}=\frac{1}{4}[(\frac{1}{2-1}-\frac{1}{{{2^2}-1}})+(\frac{1}{{{2^2}-1}}-\frac{1}{{{2^3}-1}})+…+(\frac{1}{{{2^n}-1}}-\frac{1}{{{2^{n+1}}-1}})]=\frac{1}{4}(1-\frac{1}{{{2^{n+1}}-1}})$.
点评 本题考查了等差数列与等比数列的通项公式与求和公式、数列递推关系、裂项求和方法,考查了推理能力与计算能力,属于中档题.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
| A. | $±\frac{1}{3}$ | B. | ±3 | C. | $±\frac{{2\sqrt{2}}}{3}$ | D. | $±2\sqrt{2}$ |
| A. | -4 | B. | 2 | C. | ±2 | D. | -4或2 |
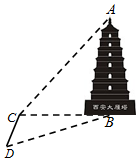 如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面
如图,某数学兴趣小组为了测量西安大雁塔高AB,选取与塔底B在同一水平面