题目内容
15.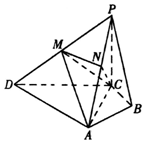 在四棱锥P-ABCD中,PC⊥底面ABCD,M,N分别是PD,PA的中点,AC⊥AD,∠ACD=∠ACB=60°,PC=AC.
在四棱锥P-ABCD中,PC⊥底面ABCD,M,N分别是PD,PA的中点,AC⊥AD,∠ACD=∠ACB=60°,PC=AC.(1)求证:PA⊥平面CMN;
(2)求证:AM∥平面PBC.
分析 (1)推导出MN∥AD,PC⊥AD,AD⊥AC,从而AD⊥平面PAC,进而AD⊥PA,MN⊥PA,再由CN⊥PA,能证明PA⊥平面CMN.
(2)取CD的中点为Q,连结MQ、AQ,推导出MQ∥PC,从而MQ∥平面PBC,再求出AQ∥平面,从而平面AMQ∥平面PCB,由此能证明AM∥平面PBC.
解答 证明:(1)∵M,N分别为PD、PA的中点,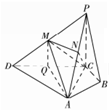
∴MN为△PAD的中位线,∴MN∥AD,
∵PC⊥底面ABCD,AD?平面ABCD,∴PC⊥AD,
又∵AD⊥AC,PC∩AC=C,∴AD⊥平面PAC,
∴AD⊥PA,∴MN⊥PA,
又∵PC=AC,N为PA的中点,∴CN⊥PA,
∵MN∩CN=N,MN?平面CMN,CM?平面CMN,
∴PA⊥平面CMN.
解(2)取CD的中点为Q,连结MQ、AQ,
∵MQ是△PCD的中位线,∴MQ∥PC,
又∵PC?平面PBC,MQ?平面PBC,∴MQ∥平面PBC,
∵AD⊥AC,∠ACD=60°,∴∠ADC=30°.
∴∠DAQ=∠ADC=30°,∴∠QAC=∠ACQ=60°,
∴∠ACB=60°,∴AQ∥BC,
∵AQ?平面PBC,BC?平面PBC,∴AQ∥平面PBC,
∵MQ∩AQ=Q,∴平面AMQ∥平面PCB,
∵AM?平面AMQ,∴AM∥平面PBC.
点评 本题考查线面垂直、线面平行的证明,考查空间中线线、线面、面面间的位置关系,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
5.执行如图的程序框图,如果输入的a=6,b=4,那么输出的s的值为( )
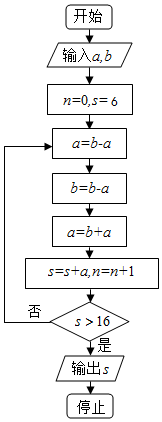

| A. | 17 | B. | 22 | C. | 18 | D. | 20 |
6.“${(\frac{1}{3})^a}<{(\frac{1}{3})^b}$”是“log2a>log2b”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
3.若函数f(x)=alog2(|x|+4)+x2+a2-8有唯一的零点,则实数a的值是( )
| A. | -4 | B. | 2 | C. | ±2 | D. | -4或2 |
10.若m=0.52,n=20.5,p=log20.5,则( )
| A. | n>m>p | B. | n>p>m | C. | m>n>p | D. | p>n>m |
7.已知a∈R,则“a<0”是“|x|+|x+1|>a恒成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
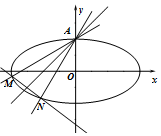 如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.
如图,已知直线l:y=kx+1(k>0)关于直线y=x+1对称的直线为l1,直线l,l1与椭圆E:$\frac{x^2}{4}+{y^2}$=1分别交于点A、M和A、N,记直线l1的斜率为k1.