题目内容
13.已知点P在函数f(x)=xex的图象上.(Ⅰ)求曲线y=f(x)在点P(1,f(1))处的切线方程;
(II)求函数y=f(x)的单调区间和极值.
分析 (Ⅰ)求得切点坐标和函数的导数,可得切线的斜率,运用点斜式方程可得切线的方程;
(II)求导,根据导数与函数单调性及极值的关系,即可求得函数y=f(x)的单调区间和极值.
解答 解:(Ⅰ)由f(x)=xex,f(1)=e,求导f′(x)=ex+xex=(1+x)ex,
∴f′(1)=2e,
∴点P(1,f(1))处的切线方程y-f(1)=f′(1)(x-1),即y-e=2e(x-1),
整理得:y=2ex-e,
曲线y=f(x)在点P(1,f(1))处的切线方程y=2ex-e;
(II)∵函数f(x)=xex的定义域为R,
f'(x)=(xex)′=x′ex+x(ex)′=ex+xex,
令f'(x)=ex+xex=ex(1+x)=0,解得:x=-1.
则x,f′(x),f(x)的变化:
| x | (-∞,-1) | -1 | (-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
当x=-1时,函数f(x)=xex的极小值为f(-1)=-$-\frac{1}{e}$,无极大值.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,利用导数求函数的单调性及极值,考查转化思想,属于中档题.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
20.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查.抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
8.已知f′(x)为函数f(x)的导函数,且$f(x)=\frac{1}{2}{x^2}-f(0)+f'(1){e^{x-1}}$,若$g(x)=f(x)-\frac{1}{2}{x^2}+x$,则方程$g(\frac{x^2}{a}-x)-x=0$有且仅有一个根时,a的取值范围是( )
| A. | [1,+∞) | B. | (-∞,1] | C. | (0,1] | D. | (-∞,0)∪{1} |
5.执行如图的程序框图,如果输入的a=6,b=4,那么输出的s的值为( )
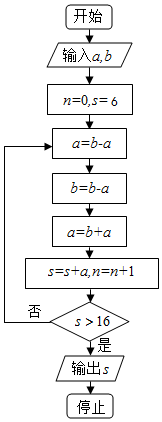

| A. | 17 | B. | 22 | C. | 18 | D. | 20 |
3.若函数f(x)=alog2(|x|+4)+x2+a2-8有唯一的零点,则实数a的值是( )
| A. | -4 | B. | 2 | C. | ±2 | D. | -4或2 |
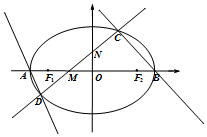 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,