题目内容
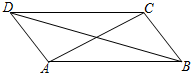 如图,平行四边形ABCD中,向量
如图,平行四边形ABCD中,向量| AC |
| 3 |
| BD |
| AC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的夹角公式、数量积运算性质、向量的三角形法则与平行四边形法则即可得出.
解答:
解:∵向量
=(1,
),
=(-2,0),
+
=
,
-
=
.
∴
=
(
-
)
=(
,
).
∴|
|=2,|
|=
=
.
•
=3.
∴cos<
,
>=
=
=
.
∴<
,
>=
.
故选:D.
| AC |
| 3 |
| BD |
| AB |
| AD |
| AC |
| AD |
| AB |
| BD |
∴
| AB |
| 1 |
| 2 |
| AC |
| BD |
=(
| 3 |
| 2 |
| ||
| 2 |
∴|
| AC |
| AB |
(
|
| 3 |
| AC |
| AB |
∴cos<
| AC |
| AB |
| ||||
|
|
| 3 | ||
2×
|
| ||
| 2 |
∴<
| AC |
| AB |
| π |
| 6 |
故选:D.
点评:本题考查了向量的夹角公式、数量积运算性质、向量的三角形法则与平行四边形法则,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列{an}的前n项和为Sn,已知a1=2,且nSn+1-(n+1)Sn=n(n+1)(n∈N+),则过A(n,an)和B(n+2,an+2)的直线的一个方向向量的坐标可以是( )
| A、(2,-4) | ||||
| B、(-1,-1) | ||||
C、(-
| ||||
D、(1,-
|
方程ln(x+1)-
=0,(x>0)的根存在的大致区间是( )
| 2 |
| x |
| A、(0,1) |
| B、(1,2) |
| C、(2,e) |
| D、(3,4) |
在(x-y)10的展开式中,系数最小的项是( )
| A、第4项 | B、第5项 |
| C、第6项 | D、第7项 |
“lgx,lgy,lgz成等差数列”是“y2=xz”成立的( )
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
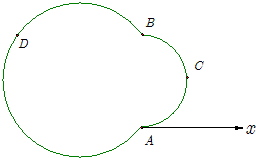 在极坐标系中,极点为A,已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成.已知B(4,
在极坐标系中,极点为A,已知“葫芦”型封闭曲线Ω由圆弧ACB和圆弧BDA组成.已知B(4,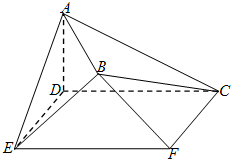 如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=
如图,在空间几何体AB-CDEF中,底面CDEF为矩形,DE=1,CD=2,AD⊥底面CDEF,AD=1,平面BEF⊥底面CDEF,且BE=BF=